自己回帰過程の定義と定常になる条件、定常自己回帰過程の性質
という記事で、定常自己回帰過程の性質を紹介しました。
その中に、逐次的に自己相関係数を算出する次の公式があります。
$$
\rho_k = \phi_1\rho_{k-1}+\phi_2\rho_{k-2}+\cdots+\phi_p\rho_{k-p}, k\geq1
$$
これをユール・ウォーカー方程式と言います。
こいつを使って、具体的に自己相関過程の自己相関係数を求めてみようというのが今回の記事です。
$p=1$や$p=2$の例は本に載っているので、$p=3$でやってみます。
$$
\rho_k = \phi_1\rho_{k-1}+\phi_2\rho_{k-2}+\phi_p\rho_{k-3}, k\geq1
$$
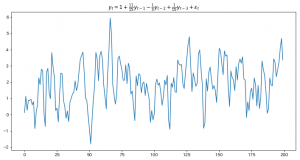
また、例として扱う定常AR(3)過程は、以前の記事でグラフをプロットした、こちらです。
$$y_t=1+\frac{11}{15}y_{t-1}-\frac{1}{3}y_{t-2}+\frac{1}{15}y_{t-3}+\varepsilon_t$$
$\phi_1,\phi_2,\phi_3$の値がわかるので、あとは、$\rho_0,\rho_1,\rho_2$さえわかれば残りの$\rho_k$は順番に計算できます。
これは、次の4つの関係式を使って計算できます。最初の2つは、ユール・ウォーカー方程式に$k=1,2$を代入したもの、
残り2つは自己相関係数の性質です。
$$
\rho_1 = \phi_1\rho_0 + \phi_2\rho_{-1} + \phi_3\rho_{-2}\\
\rho_2 = \phi_1\rho_1 + \phi_2\rho_0 + \phi_3\rho_{-1}\\
\rho_0 = 1\\
\rho_{k} = \rho_{-k}
$$
これを整理すると、
$$
\rho_1 = \phi_1 + \phi_2\rho_1 + \phi_3\rho_2\\
\rho_2 = \phi_1\rho_1 + \phi_2 + \phi_3\rho_1\\
$$
となり、さらに
$$
(1-\phi_2)\rho_1 – \phi_3\rho_2= \phi_1\\
(\phi_1+\phi_3)\rho_1 -\rho_2 =-\phi_2\\
$$
と変形できます。
あとは$\phi_k$の値を代入して、
$$
\frac{4}{3}\rho_1 – \frac{1}{15}\rho_2= \frac{11}{15}\\
\frac{4}{5}\rho_1 -\rho_2 =\frac{1}{3}\\
$$
となり、これを解くと次の二つが得られます。
$$\rho_1=\frac{5}{9},\rho_2=\frac19$$
あとは順番に代入するだけなので、pythonにやってもらいましょう。
import numpy as np
phi_1 = 11/15
phi_2 = -1/3
phi_3 = 1/15
rho_values = np.zeros(6)
rho_values[0] = 1
rho_values[1] = 5/9
rho_values[2] = 1/9
for i in range(3, 6):
rho_values[i] = phi_1*rho_values[i-1]\
+ phi_2*rho_values[i-2]\
+ phi_3*rho_values[i-3]
for rho in rho_values:
print(rho)
# 以下出力
1.0
0.5555555555555556
0.1111111111111111
-0.037037037037037035
-0.027160493827160487
-0.0001646090534979357
これで計算できました。
自己相関が指数関数的に減衰している様子も確認できます。