月: 2024年4月

pyMC5の記事の5記事目です。
今回はpyMCをつかって変更点の検出をやってみます。といっても、題材が変更点の検出というだけでメインで取り上げたいのはデータ列の途中で期待値が変わるモデルを扱いたいってのと、事後分布からのサンプリングをやりたいっていう点の2点です。

題材の紹介

題材としては、少し古い本なのですが「Pythonで体験するベイズ推論」という、キャメロン・デビッドソン=ピロンさんの本から持ってきます。これの、受信するメッセージ数の変化がテーマです。

なぜこんな古い本を題材にしたかというと、新しい本を題材にするとそのままコードを書き写す感じになるので勉強にならないからです。この本のコードはpyMC3なのでpyMC5に焼き直すとコードは大幅に変わります。

サンプルデータはこちらのリポジトリにあります。

ただ、ここからダウンロドしてくるのも手間ですし、ただの整数列なのでそのままこの記事にも書いておきます。ちなみに、全部で74日分です。

data = [13, 24, 8, 24, 7, 35, 14, 11, 15, 11, 22, 22, 11,
 57, 11, 19, 29, 6, 19, 12, 22, 12, 18, 72, 32, 9, 7, 13,
 19, 23, 27, 20, 6, 17, 13, 10, 14, 6, 16, 15, 7, 2, 15,
 15, 19, 70, 49, 7, 53, 22, 21, 31, 19, 11, 18, 20, 12, 35,
 17, 23, 17, 4, 2, 31, 30, 13, 27, 0, 39, 37, 5, 14, 13, 22
]

結果は最後に図示しますが、これ途中から件数が増えているように見えるのですよ。
それが、何日目から増えていて、その前後は期待値何件だったのか、というのをpyMCで推論していきます。

pyMCによるモデリング

ではやっていきましょう。

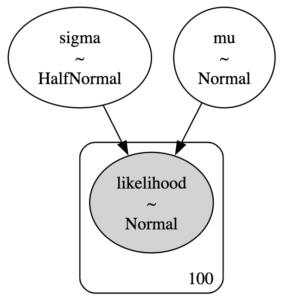
データが整数値なので、メッセージの件数はポアソン分布に従うとし、前半と後半で期待値$\lambda$が違うものとします。それぞれの$\lambda$はガンマ分布から持ってきましょう。
そして、変化する日はtauという変数名で離散一様分布からサンプリングします。

tauより前の日と以降の日で期待値が変わる点については、pm.math.switchを使って実装しました。この辺は本のコードと違います。

import matplotlib.pyplot as plt
import pymc as pm
import arviz as az


model = pm.Model()

with model:
    # 変化前の期待値
    lambda_1 = pm.Gamma('lambda_1', alpha=2, beta=1)
    # 変化後の期待値
    lambda_2 = pm.Gamma('lambda_2', alpha=2, beta=1)
    # 変化日
    tau = pm.DiscreteUniform('tau', lower=0, upper=len(data)-1)

    # idxは各データ点のインデックス
    idx = np.arange(len(data))
    # lambda_の値がtauの値によって決定される
    lambda_ = pm.math.switch(tau >= idx, lambda_1, lambda_2)
    
    # データの尤度
    obs = pm.Poisson('obs', mu=lambda_, observed=data)
    # サンプリング
    trace = pm.sample(draws=10000, tune=10000, chains=2)

サンプリングは少し多めに行っています。
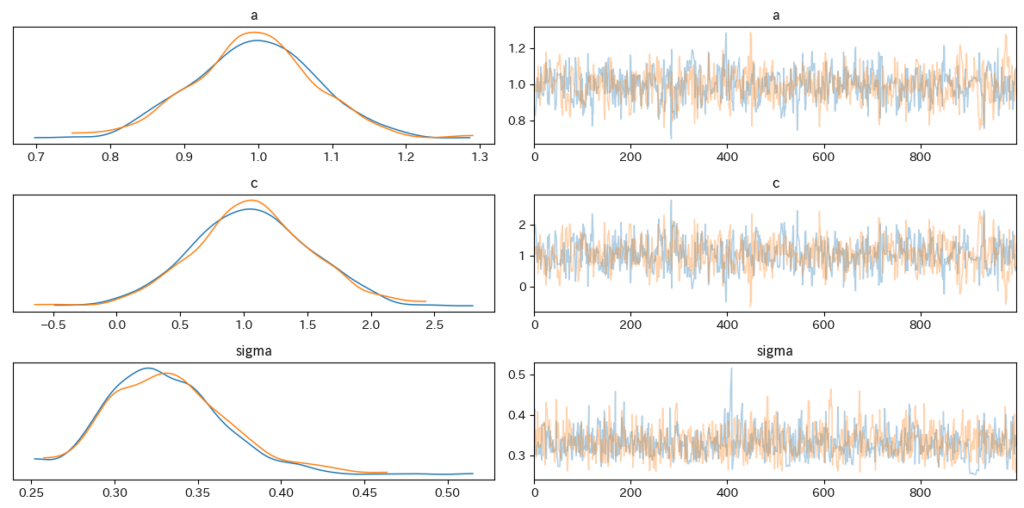
結果を見ておきましょう。

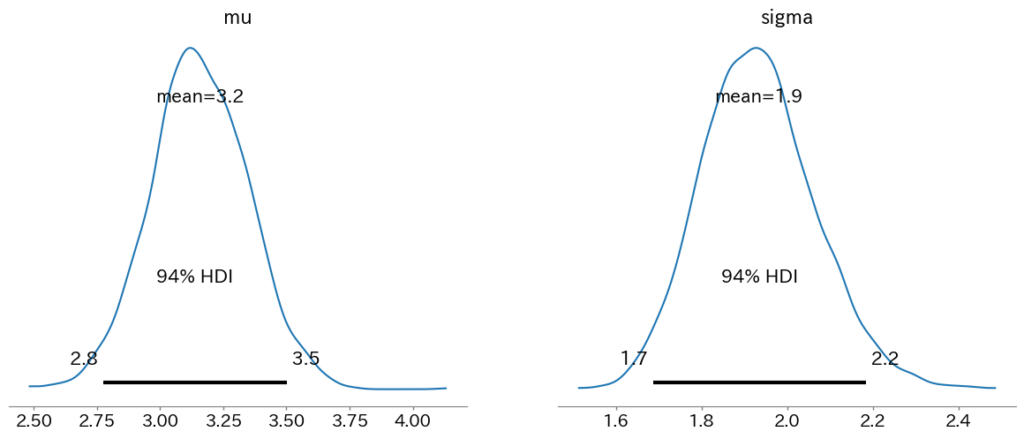
print(az.summary(trace))
"""
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
tau	43.221	0.875	42.000	44.000	0.016	0.011	3054.0	4512.0	1.0
lambda_1	17.406	0.617	16.275	18.576	0.004	0.003	18857.0	14591.0	1.0
lambda_2	22.035	0.859	20.354	23.597	0.007	0.005	15301.0	14084.0	1.0
"""

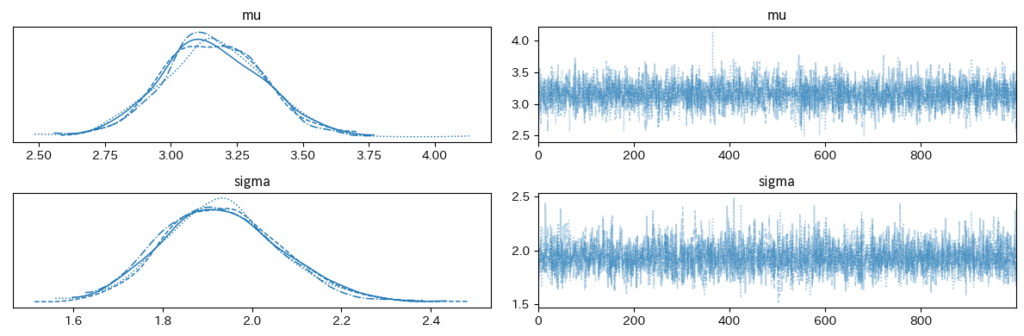
az.plot_trace(trace)
plt.tight_layout()

トレースを可視化したものがこちらです。

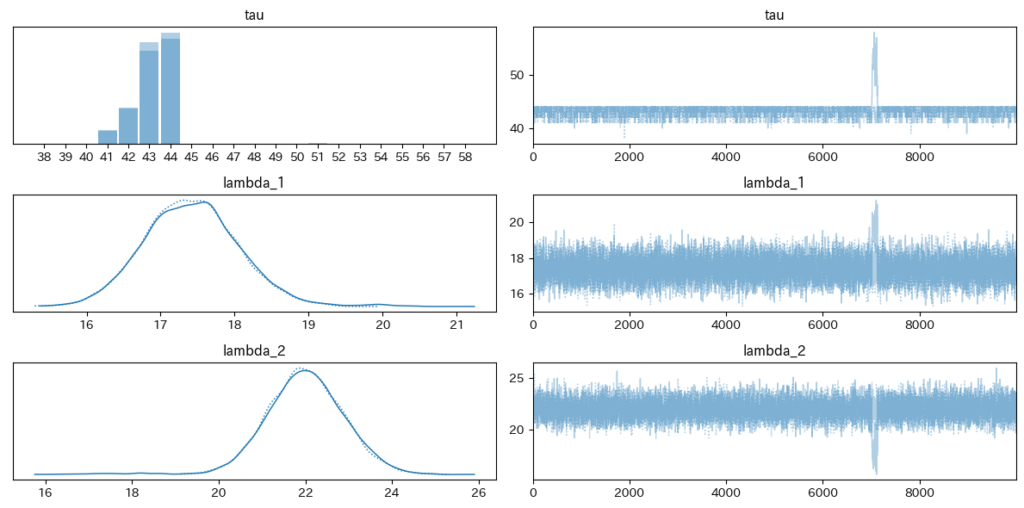
一瞬怪しいところがありますがtau = 44 あたりで変更しているのがわかりますね。

そこを閾にlambdaが増えていそうです。(17.4くらいから22くらいに。)

0日目から40日目くらいはでは、期待値17.4くらいで、45日目以降は22くらいと見て良さそうです。さて、その途中の41〜44日目はどう考えましょう？となった時に便利なのが事後分布からのサンプリングです。tauの分布を考慮していちいち計算しなくても、さっとサンプリングしてしまうことでそれぞれの日のメッセージ受信数の期待値の概算がわかります。

事後分布からのサンプリングに使うのが、 pm.sample_posterior_predictive です。これはモデルではなく、traceの方を渡してサンプリングを行います。サンプリングされるサイズが、最初に推論した時のステップ数に依存してしまうので、実はさっきサンプリングする時にdrawを大きめの値にしていたのです。draws=10000, chains=2 だったので、20000サンプルが得られます。

参考: pymc.sample_posterior_predictive — PyMC dev documentation

さて、やってみます。

# 既存のモデルとトレースを使用して、事後予測サンプルを生成
with model:
    # traceから事後予測サンプルを生成する際の修正
    posterior_predictive = pm.sample_posterior_predictive(trace, var_names=['obs'])

# 'obs'キーを使用して事後予測サンプルのデータを取得
posterior_obs = posterior_predictive.posterior_predictive['obs'].values

# 事後予測サンプルの期待値（平均）を計算
expected_values = np.mean(posterior_obs, axis=(0, 1))

axis=(0, 1) としているのは元の posterior_obs.shape が (2, 10000, 74) だからです。

これで、obsのサンプリング結果の期待値が得られました。元のデータと合わせて可視化してみましょう。

fig = plt.figure(facecolor="w")
ax = fig.add_subplot(1, 1, 1)
ax.bar(range(len(data)),data)
ax.plot(expected_values, c="orange")
plt.show()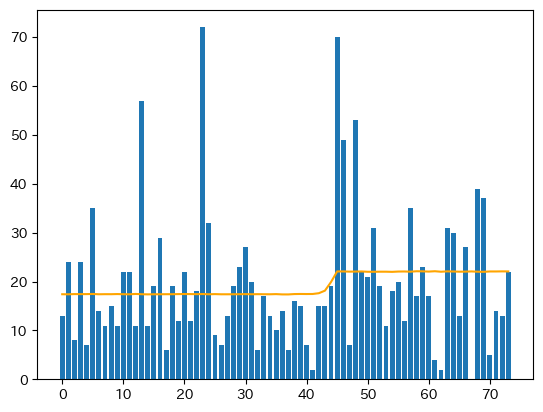

いい感じですね。

pyMCの記事4記事目です。これまでの記事では観測値だけ与えてそれを生成する確率分布を考えてきましたが、今回は観測値だけでなく何か特徴量を持つデータを考えます。
その最も単純な例として1変数の線形回帰をやってみましょう。特徴量が増えて重回帰分析になってもほとんど同じように対応できるので汎用性は高いと思います。

データの準備

何のデータを使ってもいいのですが、今回はscikit-learnのiris使います。3種類のアヤメのうち、virginicaに絞って、petal length (cm)からsepal length (cm)を予測するモデルを考えてみましょう。(相関係数が0.86くらいあって予測が簡単なのです。)

次のようにしてデータを取得します。

%%pycodestyle
import pandas as pd
from sklearn.datasets import load_iris


# irisデータ取得
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df["label"] = iris.target
# virginica に絞る
df = df[df.label == 2].reset_index(drop=True)

# 回帰分析に使う特徴量xと目的変数yを取得
x = df["petal length (cm)"].values
y = df["sepal length (cm)"].values

モデルの実装

データが揃ったらpyMCでモデルを作っていきます。

回帰係数を a, 定数項をb、誤差をε とするとモデルの式はこのようになりますね。
$$y= ax + c + \epsilon$$

ベイズで行いますので、それぞれに事前分布が必要です。
a, c の事前分布は期待値が0、標準偏差が10の正規分布としましょう。
そして、誤差項εは、期待値が0で、標準偏差がσの正規分布に従うとし、このσは標準偏差が10の半正規分布に従うとします。

これを実装してきますが、今回新たに使うのは、特徴料等の定数を格納する pm.ConstantData と 数式を定義できるpm.Deterministic です。

参考:
pymc.ConstantData — PyMC dev documentation
pymc.Deterministic — PyMC v5.6.0 documentation

正確には、 ConstantData の方は使わなくてもいいのですが、明示的に書いておくとモデルを可視化した時に定数部分も表示されるので便利です。

実際にコードを見ていただくと使い方がわかると思うのでやっていきましょう。例によって、Graphvizで可視化してJpyterで表示しています。

import numpy as np
import matplotlib.pyplot as plt
import pymc as pm
import arviz as az


model = pm.Model()

with model:
    x_data = pm.ConstantData("x_data", x)
    y_data = pm.ConstantData("y_data", y)

    # 回帰係数と定数項
    a = pm.Normal("a", mu=0, sigma=10)
    c = pm.Normal("c", mu=0, sigma=10)

    # yの期待値
    mu = pm.Deterministic("mu", a*x_data + c)
    # 誤差
    sigma = pm.HalfNormal("sigma", sigma=10)

    # 観測値
    obs = pm.Normal("obs", mu=mu, sigma=sigma, observed=y_data)

# モデルの可視化
g = pm.model_to_graphviz(model)
display(g)

参考ですが、ConstantDataを使わない場合はこうなります。

model2 = pm.Model()

with model2:

    # 回帰係数と定数項
    a = pm.Normal("a", mu=0, sigma=10)
    c = pm.Normal("c", mu=0, sigma=10)

    # yの期待値
    mu = pm.Deterministic("mu", a*x + c)
    # 誤差
    sigma = pm.HalfNormal("sigma", sigma=10)

    # 観測値
    obs = pm.Normal("obs", mu=mu, sigma=sigma, observed=y)

g = pm.model_to_graphviz(model2)
display(g)

モデルができたのでサンプリングして結果を見ていきましょう。

with model:
    trace = pm.sample(random_seed=42, chains=2)


display(az.summary(trace, var_names=["a", "c", "sigma"]))
"""
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a	0.995	0.084	0.828	1.143	0.003	0.002	641.0	636.0	1.0
c	1.066	0.470	0.216	1.988	0.019	0.013	648.0	679.0	1.0
sigma	0.331	0.035	0.259	0.391	0.001	0.001	554.0	349.0	1.0
"""

az.plot_trace(trace, var_names=["a", "c", "sigma"], compact=False)
plt.tight_layout()

いい感じに推定できていますね。

回帰直線の可視化

せっかく単回帰したので、回帰直線を可視化してみたいと思います。上記のsummaryのa,cで可視化してもいいのですがせっかくなのでサンプリングの各ステップの値で可視化してみましょう。

# a, cの各ステップの値を取得
a_list = trace.posterior.a.values.ravel().reshape(-1, 1)
c_list = trace.posterior.a.values.ravel().reshape(-1, 1)

# xの範囲
x_values = np.array([4.4, 7.0])

# a, c の各値からyの値を計算
y_preds = x_values * a_list + c_list

# 回帰直線と元のデータを可視化
for y_pred in y_preds:
    plt.plot(x_values, y_pred, lw=1, alpha=0.01, c="c")
plt.scatter(x, y)
plt.show()

なかなか妥当な結果が得られましたね。

まとめ

今回は線形回帰を題材として取り上げましたが、線形回帰に限らず特徴量を使うモデリングは同じようにして実装していくことができます。pm.Deterministicを使うと一気に実装の幅が広がりますのでぜひ試してみてください。

pyMCの3つ目の記事です。

このブログではまだ超単純なものしか扱っていませんが、pyMCではかなり柔軟にモデルを構築できます。そうなってくると、自分が実装したモデルが妥当なものなのか、思うような事象を表現できているのかといったことをサンプリング前に確認しておきたくなるものだと思います。

そのような場合に備えて、pyMCでは、ベイズ推論を行う前に事前分布からそのままサンプリングを行い結果を確認するメソッドとして、 pm.sample_prior_predictive() というものが用意されています。
参考: pymc.sample_prior_predictive — PyMC dev documentation

使い方は簡単で、モデルを組んだ後にsample()の代わりにこれを呼び出すだけです。引数としてはサンプリングしたいデータ数を渡します。

では具体的にやってみましょう。今回は二項分布あたりを扱ってみましょうかね。$n=10$くらいで、$p$は0から1の一様分布からサンプリングしてみましょう。通常二項分布って$np$を期待値として山形になるのですが、$p$が固定されていないのでそうはならない例をお見せできると思います。

import pymc as pm
import arviz as az
import matplotlib.pyplot as plt


with pm.Model() as model:
    # 事前分布を設定
    p = pm.Uniform('p', lower=0, upper=1)
    y = pm.Binomial('y', n=10, p=p)

    # 事前分布からサンプリング
    prior_predictive = pm.sample_prior_predictive(samples=1000)

このサンプリングはかなり短時間で終わります。複雑なモデルの通常のサンプリングは結構時間がかかるので、その意味でも事前確認をしておくメリットはありますね。

サンプリングしたら結果を確認します。prior_predictive って変数に結果が確認されていますが、`prior_predictive.prior[“p”]`や`prior_predictive.prior[“y”]`のような形式でサンプリング結果を取り出せます。

arviz使って確認しましょう。

fig = plt.figure(figsize=(12, 5), facecolor="w")
ax = fig.add_subplot(1, 2, 1, title="p")
az.plot_dist(prior_predictive.prior["p"], ax=ax)
ax = fig.add_subplot(1, 2, 2, title="y")
az.plot_dist(prior_predictive.prior["y"], ax=ax)
plt.show()

結果がこちらです。

サンプルサイズ(1000と設定しました。デフォルトは500です。)が小さいのか、ちょっとpの分布がボコボコしていますが概ね想定通りの結果が得られましたね。

pyMCの記事2記事目です。
前回非常にシンプルなモデルで推論をやりましたが、今回はその結果を可視化する便利なライブラリである、ArviZの紹介です。

ArviZはpyMCに限らず、ベイズモデルの分析や可視化、比較等を行うライブラリです。ベイズ推論の結果の分析に特化しているだけあって非常に多くの機能を持っています。
参考: ArviZ: Exploratory analysis of Bayesian models — ArviZ 0.18.0 documentation

今回は特に利用頻度が高いと思われるメソッドに絞って紹介していきます。

例としては前回の記事で作った単純なモデルを使います。前回のコードを走らせてサンプリングした結果が trace という変数に入ってるという前提で見ていってください。

参考: PyMC version 5 超入門

推論結果のサマリーをまとめる

最初に紹介するのは推論結果を統計値で返してくれる、az.summary()です。これだけは可視化ではない(グラフ等での表示ではない)のですがよく使うのでこの記事で紹介します。
参考: arviz.summary — ArviZ 0.18.0 documentation

pm.summary()とほとんど同じ挙動なのですが、トレース結果の統計値をDataFrame形式で返してくれます。

import pymc as pm
import arviz as az


az.summary(trace)
#　以下結果
"""
mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	3.157	0.192	2.774	3.501	0.003	0.002	4182.0	2738.0	1.0
sigma	1.933	0.133	1.687	2.184	0.002	0.002	3934.0	3009.0	1.0
"""

各変数の平均値等が確認できるので便利ですね。

サンプルの系列(トレース)を可視化する

次に紹介するのは az.plot_trace()です。MCMCの可視化としては一番ポピュラーなやつではないでしょうか。
参考: arviz.plot_trace — ArviZ 0.18.0 documentation

今回用意している例では2変数を4系列で1000ステップサンプリングしていますので、その分布とトレースを一気に可視化してくれます。
手元で試したところ、ちょっとラベルが重なっていたので、matplotlibのメソッドを一つ呼び出して調整しています。

import matplotlib.pyplot as plt


az.plot_trace(trace)
plt.tight_layout()
plt.show()

出力結果がこちらです。

いい感じですね。

事後分布を可視化する

さっきのトレースの左半分にも表示されてはいるのですが、本当に欲しい結果は事後分布です。それを表示することに特化しているのが az.plot_posterior() です。
参考: arviz.plot_posterior — ArviZ 0.18.0 documentation

やってみます。

az.plot_posterior(trace)
plt.show()

出力がこちら。事後分布と変数名、期待値等やhdiなどを可視化してくれましたね。

フォレストプロットで可視化する

フォレストプロットとは何か？というのは実物を見ていただいた方が早いと思うのでやってみます。2変数なのでいまいちありが分かりにくいと思いますが、変数の数が多いとこれは非常に便利です。
参考: arviz.plot_forest — ArviZ 0.18.0 documentation

az.plot_forest(trace)
plt.show()

結果がこちら。

サンプリングの系列ごとに可視化してくれていますね。引数で、 combined=True を一緒に渡すと、系列をまとめて変数ごとに集計してくれますよ。

kind等の引数で見た目を変えていくこともできるのでドキュメントを参照していろいろ試してみてください。

分布を可視化する

最後は、ちょっと特殊です。AzviZにはnumpyの配列などを受け取って単純に分布を表示するメソッドなども用意されています。それが、az.plot_dist()です。
参考: arviz.plot_dist — ArviZ 0.18.0 documentation

これは、numpy配列(要するにarray)を受け取るので、先ほどまでの例のようにtraceをそのまま渡せません。pyMCの事後分布を可視化したいのであれば、traceからサンプリングした結果の部分を自分で取り出して渡す必要があります。

例えば、muの方であればこのようになります。

az.plot_dist(trace.posterior['mu'].values.ravel())
plt.show()

結果がこちら。

これはpyMCの結果以外でも汎用的に使えるやつなので一緒に紹介しました。

その他の補足

今回の記事では、例としたモデルが非常に単純だったので使いませんでしたが、大規模なものになると全変数表示すると潰れてしまって読み取れないということが起きます。
そのような場合、それぞれのメソッドが var_names という引数で出力する変数を絞り込めるようになっているで使ってみてください。

また、多くのメソッドは ax 引数などを受け取れるようになっているで、出力先のaxを指定してmatplotlibの機能で出力を加工することなどもできます。

それ以外にも各メソッドさまざまなオプションを持っているのでぜひドキュメントを参照しながら使いこなしてみてください。

半年ほど前から、PyMCを使うようになりました。だいぶ慣れてきたのでこれから数回の記事でPyMCの入門的な内容をまとめていこうと思います。(記事執筆時間の制約等の要因で途中で違うテーマの記事を挟むかもしれませんができるだけ連続させたいです。)

PyMCとは

PyMCはPythonで書かれたオープンソースの確率的プログラミングライブラリです。ベイズ統計モデルを構築、分析し、複雑な統計的問題を解くことができます。PyMCのversion4の開発ではいろいろゴタゴタがありバージョン番号がスキップされたようですが、現在ではverison5がリリースされています。

公式ドキュメントはこちらです。
参考: Home — PyMC project website

特徴としては、線形モデルから複雑な階層モデルまで、幅広いモデルを柔軟に構築できることや、最新のMCMCアルゴリズムを利用して、効率的にサンプリングが行えることが挙げられます。

ただし、柔軟にモデルを構築できる反面で、自分でモデルの内容を実装しないといけないのでscikit-learnのような、既存のモデルをimportしてfit-predictさせたら完結するような単純なAPIにはなっていません。それでも、かなり直感的なAPIにはなっていると感じています。

サンプルコード

一番最初の記事なので、今回は本当に一番単純なサンプルコードを紹介します。これは正規分布に従う標本を生成して、そのパラメーターを推定するというものです。

ダミーデータは平均3, 標準偏差2の正規分布から取りました。

ベイズ推定するので、パラメーターに事前分布が必要です。これは平均の方は平均0、標準偏差10の正規分布、標準偏差の方はsigma=10の半正規分布を設定しました。

ダミーデータ生成からモデルの作成までが以下のコードです。

import pymc as pm
import numpy as np

# ダミーデータを生成
true_mu = 3
true_sigma = 2
np.random.seed(seed=10)
data = np.random.normal(true_mu, true_sigma, size=100)

with pm.Model() as model:
    # 事前分布を設定
    mu = pm.Normal('mu', mu=0, sigma=10)
    sigma = pm.HalfNormal('sigma', sigma=1)

    # 尤度関数を設定
    likelihood = pm.Normal('likelihood', mu=mu, sigma=sigma, observed=data)

ダミーデータの生成分は単純なのでいいですね。
その後が本番です。
PyMCでは、withを使ってコンテキストを生成し、その中に実際のコードを書いていきます。
pm.Normal や pm.HalfNormal など、さまざまな確率分布が用意されていますが、それを使って変数の事前分布を定義しています。

そして、そこで事前分布を設定された変数、mu, sigmaを使って最後の正規分布を定義し、観測値(observed)として用意したダミーデータを渡しています。

Graphvizを導入している環境の場合、次のようにしてモデルを可視化できます。
これはコンテキストの外で行えるので注意してください。(displayしていますが、これはjupyter上に表示することを想定しています。)

g = pm.model_to_graphviz(model)
display(g)

出力結果がこちらです。

モデルが出来上がったらサンプリングを行います。

サンプリングはコンテキスト内で、pm.sample()メソッドを呼び出すことで行います。
引数としては初期の捨てるサンプル数(tune)と、分析に利用するサンプル数(draws)、さらにサンプル値系列を幾つ生成するかを示すchainsを渡します。

with model:
    trace = pm.sample(
        draws=1000,
        tune=1000,
        chains=4,
    )

# 以下出力。時間がかかる処理の場合プログレスバーも見れるので助かります。
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sigma]

 100.00% [8000/8000 00:00<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

サンプルが終わったら要約を表示します。

# サンプルの要約を表示
summary = pm.summary(trace)
print(summary)

# 結果
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	3.155	0.191	2.792	3.506	0.003	0.002	3867.0	2867.0	1.0
sigma	1.933	0.135	1.687	2.191	0.002	0.002	3927.0	3150.0	1.0

meanの値を見ると、それぞれ真の値に結構近い値が得られていますね。

以上が、本当に一番シンプルなPyMCの使い方の記事でした。

今後の記事ではもう少し細かい仕様の話や発展的な使い方、ArviZという専用の可視化ライブラリの話などを紹介していきたいと思います。