HITSアルゴリズム(Hyperlink-Induced Topic Search)という手法がありますので紹介します。
NetworkXのドキュメントにおいて、PageRankと一緒に Link Analysis のページにあることから存在を知りました。
参考: NetworkXのドキュメントの Link Analysis
論文: A Survey of Eigenvector Methods for Web Information Retrieval (Amy N. Langville, Carl D. Meyer)
Wikipedia: HITS algorithm
まずおさらいですが、PageRankの発想は、「重要なページからリンクされているページは重要」というものでした。
そして、各ページはそれぞれ一つのスコア(PageRank)を持ちます。
PageRankの特徴として、リンクが増えると、リンクされている側のページのスコアは上がりますが、
リンク元のページにはなんら恩恵がありません。
しかし実際、優良なページに多くのリンクを貼っているのであれば、そのページも便利なページではあります。いわゆるリンク集やナビサイトです。
この、優良なページにたどり着くことを容易にするページも評価しようとしているのが、HITSアルゴリズムです。
HITSアルゴリズムは、それぞれのページに Hub(ハブ値) と Authority(権威値) という二つのスコアを付与します。
Authority の方が、PageRankに近い概念で、Hubの方は、優良なページにリンクを飛ばすと高くなる値になります。
実際の計算式に近い形でまとめて説明すると、HITSアルゴリズムは次の二つの要素からなります。
– Hubが高いページからリンクされるほど、Authorityが高くなる。
– Authorityが高いページへリンクするほど、Hubが高くなる。
ここ最近の固有ベクトル中心性やPageRankの記事を読んでいただけていたら予想がつくと思うのですが、
これらの計算も行列の掛け算の繰り返しが収束することによって求まります。
そして、行列の固有ベクトルとして算出することもできます。
まず、$i$番目のノードから$j$番目のノードにリンクがある時に$(i, j)$成分が$1$に、そうでない時に$0$になる隣接行列を$L$とおきます。
数式で書くと以下の通りです。
$$
\mathbf{L} = \{a_{i, j}\} =
\left\{ \begin{align}1 (iからjにリンク有り)\\0 (iからjにリンク無し)\end{align}\right.
$$
(文献によって、定義が転置していたり、値が正規化されていたりするのでご注意ください。)
そして、それぞれのノードのハブ値のベクトル$\mathbf{h}^{(k)}$と、権威値のベクトル$\mathbf{a}^{(k)}$を次のように初期化します。
$\mathbf{1}$は全ての要素が1のベクトル、$N$はノード数です。
$$
\mathbf{h}^{(0)} = \mathbf{a}^{(0)} = \mathbf{1}/N.
$$
定義に沿って、ハブ値と、権威値を再帰的に計算するには、次の操作を繰り返すことになります。($\cdot$は行列積です)
$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{h}^{(k-1)} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{a}^{(k-1)} \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$
さて、numpyでこの通り実装し、ループを回して計算すると$\mathbf{h}^{(k)}$も$\mathbf{a}^{(k)}$も一定値に収束することは容易に観測されます。
一応、ランダムに生成したグラフに対して、上の数式の通りに計算して確認しておきましょう。
import numpy as np
import networkx as nx
# ランダムに有向グラフ生成
G = nx.random_graphs.fast_gnp_random_graph(n=10, p=0.2, directed=True)
# 隣接行列取得
L = nx.to_numpy_array(G)
print(L)
"""
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 1. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 1. 1. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[1. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 1. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 1. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 1. 0. 1. 0. 0. 0.]]
"""
# ハブ値と権威値を初期化
hubs = np.ones(shape=nx.number_of_nodes(G))/nx.number_of_nodes(G)
authorities = np.ones(shape=nx.number_of_nodes(G))/nx.number_of_nodes(G)
# 再帰的に計算する。
for _ in range(40):
# ハブ値から権威値を計算する。
authorities = hubs @ L
# 権威値からハブ値を計算する。
hubs = authorities @ L.T
# 標準化
hubs /= sum(hubs)
authorities /= sum(authorities)
print("authorities: ", authorities.round(3))
print("hubs:", hubs.round(3))
"""
authorities: [0.105 0. 0.105 0.105 0.158 0.158 0.053 0.158 0.105 0.053]
hubs: [0. 0.156 0.156 0.067 0.067 0.089 0.2 0.156 0.022 0.089]
authorities: [0.097 0. 0.097 0.124 0.142 0.204 0.035 0.168 0.124 0.009]
hubs: [0. 0.172 0.168 0.057 0.068 0.079 0.208 0.172 0.004 0.072]
authorities: [0.097 0. 0.097 0.131 0.13 0.213 0.028 0.172 0.131 0.001]
hubs: [0. 0.178 0.175 0.052 0.069 0.078 0.207 0.178 0.001 0.063]
-- (中略) --
authorities: [0.1 0. 0.1 0.138 0.116 0.216 0.021 0.172 0.138 0. ]
hubs: [0. 0.183 0.18 0.047 0.069 0.081 0.203 0.183 0. 0.055]
authorities: [0.1 0. 0.1 0.138 0.116 0.216 0.021 0.172 0.138 0. ]
hubs: [0. 0.183 0.18 0.047 0.069 0.081 0.203 0.183 0. 0.055]
"""
この、最後の方で収束している値が、この記事のテーマのハブ値と権威値です。
Networkxで計算することもできるので見ておきましょう。
PageRank同様に複数の実装がありますが、 numpyで実装された、hits_numpyを使えば十分でしょう。
h, a = nx.hits_numpy(G)
print(h)
"""
{0: 0.0,
1: 0.1828404557137138,
2: 0.18031994425802442,
3: 0.04654212497804568,
4: 0.06918950852466288,
5: 0.08062191959815146,
6: 0.20269591155066588,
7: 0.1828404557137138,
8: 0.0,
9: 0.054949679663021944}
"""
print(a)
"""
{0: 0.1000629943543116,
1: -0.0,
2: 0.10006299435431144,
3: 0.13792829814529123,
4: 0.11553047637984128,
5: 0.21586948330461359,
6: 0.020869885042915804,
7: 0.17174757027342366,
8: 0.1379282981452913,
9: -0.0}
"""
さて、例によって、再帰的に計算して、収束を待つというのは非常にコストの高い計算なので、もう少し効率化を考えます。
先ほどの計算式をよく見ると、$\mathbf{h}^{(k)}$と$\mathbf{a}^{(k)}$は相互に計算するのではなく、
自分自身の前の状態から計算できることがわかります。少し変形するとこうですね。
$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{a}^{(k-2)} \cdot L^{\top} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{h}^{(k-2)} \cdot L \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$
$k=0$から計算が始まるので、この式からは偶数番目の項しか出てきませんが、収束先は同じですので無視してしまって、次の漸化式の収束先を考えましょう。
$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{a}^{(k-1)} \cdot L^{\top} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{h}^{(k-1)} \cdot L \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$
すると、固有ベクトル中心性やPageRank時と同じように、$\mathbf{h}^{(k)}$も$\mathbf{a}^{(k)}$も、その収束先を、
行列の最大固有値に対する固有ベクトルとして算出できます。
具体的には、
ハブ値$\mathbf{h}^{(k)}$のほうは、 $(L \cdot L^{\top})^{\top} = L \cdot L^{\top}$ の固有ベクトル、
権威値$\mathbf{a}^{(k)}$のほうは、 $(L^{\top} \cdot L)^{\top} = L^{\top} \cdot L$ の固有ベクトル、
として、求まります。
hub_eig = np.linalg.eig(L@L.T)[1][:, 0]
hub_eig /= sum(hub_eig)
print(hub_eig.round(3))
# [0. 0.183 0.18 0.047 0.069 0.081 0.203 0.183 0. 0.055]
authority_eig = np.linalg.eig(L.T@L)[1][:, 0]
authority_eig /= sum(authority_eig)
print(authority_eig.round(3))
# [ 0.1 -0. 0.1 0.138 0.116 0.216 0.021 0.172 0.138 -0. ]
バッチリ算出できました。固有ベクトル本当に便利ですね。
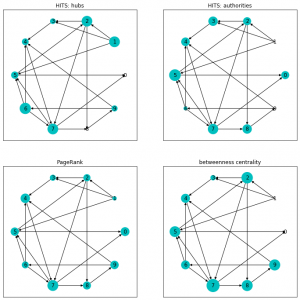
最後に、ノードのサイズとして両指標を可視化しておきましょう。
比較用にPageRankと媒介中心性も入れました。
import matplotlib.pyplot as plt
# ハブ値と権威値算出
h_dict, a_dict = nx.hits_numpy(G)
h_list = np.array([h_dict[n] for n in G.nodes])
a_list = np.array([a_dict[n] for n in G.nodes])
# PageRankと媒介中心性も算出
pr_dict = nx.pagerank_numpy(G)
pr_list = np.array([pr_dict[n] for n in G.nodes])
bc_dict = nx.betweenness_centrality(G)
bc_list = np.array([bc_dict[n] for n in G.nodes])
# 可視化
fig = plt.figure(figsize=(12, 12), facecolor="w")
ax = fig.add_subplot(221, title="HITS: hubs")
nx.draw_networkx(G, pos=pos, node_size=3000*h_list, ax=ax, node_color="c")
ax = fig.add_subplot(222, title="HITS: authorities")
nx.draw_networkx(G, pos=pos, node_size=3000*a_list, ax=ax, node_color="c")
ax = fig.add_subplot(223, title="PageRank")
nx.draw_networkx(G, pos=pos, node_size=3000*pr_list, ax=ax, node_color="c")
ax = fig.add_subplot(224, title="betweenness centrality")
nx.draw_networkx(G, pos=pos, node_size=3000*bc_list, ax=ax, node_color="c")
PageRankではほとんど評価されていない1番のノードが、Hubとしてきちんと評価されていること、
それによって1番からリンクを得ている、2,3,5が、PageRankに比べて、権威値が高くなっていることなど確認できますね。
実験する前は PageRank と 権威値 はもっと似てる結果になると思っていたのですが、
(確かに似てはいるけど) 予想よりも指標の特徴がいろいろ出ていますね。