前回の記事に引き続き、グラフのノードの中心性の話です。
参考: ネットワークグラフの中心性
前回紹介した3種類の中心性はノード間のつながり方によってのみ算出されましたが、
それぞれのノードは対等に扱っていました。
例えば、次数中心性では、何個のノードとつながっているかのみを気にしており、つながっているノードの性質は気にしていません。
しかし、ノードの重要度を図る上で、同じ数のノードに繋がっているとしても、
より重要なノードと繋がっている方が需要と考えることは自然なことです。
この、重要なノードとつながっているものの方が重要であると言う概念を取り入れた中心性が、
固有ベクトル中心性(eigenvector centrality)です。
これを説明したいのですが、ちょっと複雑なので、
最初に次のようなゲームを考えてみましょう。
1. 初期の状態(t=0)において、各ノードはそれぞれ等しいポイントを持っている。
2. 次の状態(tが1増える)において、各ノードは、自分のポイントを繋がっている全てのノードに渡す。
(有向グラフの場合は、矢印の向きにのみ渡します。)
各ノードは、受け取ったポイントの合計を自分のポイントとする。
3. 2を繰り返す。
これなら、たくさんのノードとつながっていると、どんどんポイントをもらえます。
また、たくさんポイントを持っているノードとつながっていると有利です。
具体的にこれを計算してみるのですが、その前に隣接行列(adjacency matrix)という概念を導入しておきます。
これは、グラフGに対して定まる$n\times n$($n$はグラフのノード数)行列で、
$i$番目のノードから$j$番目のノードに向かって辺が伸びていたら、$(i, j)$成分が$1$、そうでなければ$0$になるものです。
(無向グラフの場合は、対称行列になります)
networkxには、隣接行列を取り出す関数がたくさん用意されています。(結果のデータ型が少しずつ違います。)
自分がよく使うのを二つだけ紹介します。この記事では、to_numpy_arrayの方を使います。
nx.to_numpy_array() # numpyのarray型で返す。グラフが小さい時はこれがオススメ.
nx.adjacency_matrix(G) # これは scipyの疎行列の型で返します。グラフが大きい時はこちら。
import networkx as nx
import numpy as np
while True:
# ランダムにグラフを生成する
G = nx.random_graphs.fast_gnp_random_graph(
n=7,
p=0.3,
directed=False
)
# 連結なグラフが生成できたらループを抜ける
if nx.is_connected(G):
break
# 隣接行列 (i番目からj番目のノードにパスがある時、(i, j)成分が1)
adj_matrix = nx.to_numpy_array(G)
print(adj_matrix)
"""
[[0. 0. 0. 1. 1. 0. 0.]
[0. 0. 1. 1. 0. 0. 0.]
[0. 1. 0. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 0. 1.]
[1. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0.]]
"""
さて、隣接行列を何に使うかというと、先ほど定義したゲームの手順2のポイントの受け渡しです。
これは、for文を回して愚直に計算すると結構面倒なのですが、なんと、ポイントのベクトルにこの連結行列をかけるだけで実装できてしまします。
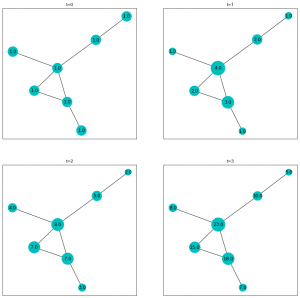
全てのノードのポイントが1から初めて、$t=3$までやってみましょう。
import matplotlib.pyplot as plt
# 配置を固定しておく
pos = nx.spring_layout(G)
# 各ノードに等しい点を与える。
points_list = []
points_list = [np.ones(shape=G.number_of_nodes())]
for i in range(3):
# ポイントベクトルに隣接行列を掛けたものが次の状態のポイントベクトル
points_list.append(points_list[i]@adj_matrix)
# グラフを可視化
fig = plt.figure(figsize=(14, 14), facecolor="w")
for i in range(0, 4):
ax = fig.add_subplot(2, 2, i+1, title=f"t={i}")
nx.draw_networkx(
G,
ax=ax,
node_color="c",
pos=pos,
node_size=700 * points_list[i] / np.mean(points_list[i]),
labels=dict(zip(G.nodes, points_list[i])),
)
plt.show()
出力がこちら。
このゲームのルールが、ポイントベクトルと隣接行列の積で再現できてることが確認できます。
さて、ご覧の通り、これを延々と続けていくと、各ノードのポイントがどこまでも大きくなってしまいます。
これを防ぐために、ポイントはl2ノルムで正規化することにしましょう。(要するにポイントベクトルの長さが1になるように縮めます。)
すると、面白いことに、この操作を繰り返すとポイントが一定の値に収束します。
# 各ノードに等しい点を与える。
points = np.ones(shape=G.number_of_nodes())
# l2正規化
points /= np.linalg.norm(points)
for _ in range(30):
# 隣接行列をかける
points = points@adj_matrix
# l2正規化
points /= np.linalg.norm(points)
print(points.round(3))
"""
[0.333 0.333 0.5 0.667 0.167 0.167 0.167]
[0.34 0.476 0.476 0.544 0.136 0.204 0.272]
[0.276 0.413 0.496 0.634 0.138 0.193 0.221]
-- 中略 --
[0.288 0.444 0.502 0.596 0.116 0.203 0.241]
[0.288 0.444 0.502 0.596 0.116 0.203 0.241]
[0.288 0.444 0.502 0.596 0.116 0.203 0.241]
"""
この値こそが、記事タイトルにあげた、固有ベクトル中心性です。
何故このような名前になっているかというと、この値は隣接行列(の、転置行列の)の最大固有値に対する固有ベクトルとして算出できるからです。
無限ループさせて収束を観測するのは、大きなグラフでは大変なので、とてもありがたい性質ですね。
今回は無向グラフを使っているので、 .Tして、転置を取らなくても結果は同じですが、
有向グラフでは転置を取る必要があるのでサンプルコードにも入れておきました。
実際に、numpyで固有ベクトルを計算してみて見比べてみましょう。
eigen_vector = np.abs(np.linalg.eig(adj_matrix.T)[1][:, 0])
print(eigen_vector.round(3))
# [0.288 0.444 0.502 0.596 0.116 0.203 0.241]
確かに同じ値になっています。(符号が逆のベクトルが戻ってくることがあるので、np.absで絶対値取っています。)
(この記事の本題ではないですが、np.linalg.eig は使い方になかなかクセがありますね。
そのうち個別にまとめたいです。)
networkxにも、固有ベクトル中心性を求める関数は準備されています。しかも二つ。
eigenvector_centrality
eigenvector_centrality_numpy
それぞれ、numpyを使わない実装と使う実装のようです。
eigenvector_centrality_numpy の方がメリットが多いようなので、numpyも入っている環境ならこちらを使いましょう。
どちらも結果がdict型なので、使う時はその点だけ注意です。
print(nx.eigenvector_centrality_numpy(G))
"""
{
0: 0.2878634949610299,
1: 0.4438129053071405,
2: 0.5022278145024875,
3: 0.5959832042188999,
4: 0.1163324095757721,
5: 0.20296207348193807,
6: 0.24085083182520173
}
"""
この固有ベクトル中心性は、重要なものの近くが重要という再帰的な定義がきっちり計算できる点で数学的にも面白いです。
ただ、いくつか欠点があります。
今回の例は連結な無向グラフを扱いましたが、そうでない場合、つまり有向グラフや孤立したノードがある場合に問題が発生します。
例えば、どの点からも流入がないノードはすぐポイントが0になってしまい、
さらにそのような点からしかパスが通ってないところは連鎖的に0点になってしまいます。
行き止まりの存在も課題です。
次の記事ではこのあたりの問題への対応を紹介する予定です。