何らかのデータ(標本)が、特定の確率分布に従ってるかどうかを検定したいことって頻繁にあると思います。そのような場合に使えるコルモゴロフ–スミルノフ検定(Kolmogorov–Smirnov test, KS検定)という手法があるのでそれを紹介します。
取り上げられている書籍を探したのですが、手元に見当たらなかったので説明はWikipediaを参照しました。コルモゴロフ–スミルノフ検定 – Wikipedia
1標本と、特定の確率分布についてその標本が対象の確率分布に従っていることを帰無仮説として検定を行います。
この記事では、scipyを使った実装と、それを理解するための検証をやっていきたいと思います。
とりあえずこの記事で使うライブラリをインポートし、データを準備します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import kstest
from scipy.stats import kstwo
from scipy.stats import t
from scipy.stats import norm
norm_frozen = norm.freeze(loc=10, scale=10) # 検定する分布
t_frozen = t.freeze(df=5, loc=10, scale=10) # 標本をサンプリングする分布
t_samples = t_frozen.rvs(size=1000, random_state=0) # 標本を作成
# 各データを可視化
xticks = np.linspace(-40, 60, 1001)
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(1, 1, 1)
ax.plot(xticks, norm_frozen.pdf(xticks), label="正規分布")
ax.plot(xticks, t_frozen.pdf(xticks), label="t分布")
ax.hist(t_samples, density=True, bins=50, alpha=0.5, label="t分布からの標本")
ax.legend()
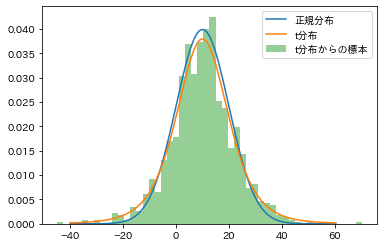
plt.show()作成された図がこちらです。流石にt分布と正規分布は似ていますね。ぱっと見でこの標本が正規分布に従ってないと言い切るのは難しそうです。
それでは、早速scipyで(1標本)KS検定をやっていきましょう。これは専用の関数が用意されているので非常に簡単です。scipy.stats.kstest — SciPy v1.9.0 Manual
rvs引数に標本データ、cdf引数に検定したい分布の累積分布関数を指定してあげれば大丈夫です。alternative で両側検定、片側検定などを指定できます。今回は両側で行きます。有意水準は0.05としましょう。
ks_result = kstest(rvs=t_sample, cdf=norm_frozen.cdf, alternative="two-sided")
print(ks_result)
# KstestResult(statistic=0.04361195130340301, pvalue=0.04325168699194537)
# 統計量と引数を変数に入れておく
ks_value = ks_result.statistic
p_value = ks_result.pvalueはい、p値が約0.043 で0.05を下回ったので、この標本が正規分布にし違うという帰無仮説は棄却されましたね。
ちなみに、標本をサンプリングした元のt分布でやると棄却されません。これも想定通りの挙動ですね。
print( kstest(rvs=t_sample, cdf=t_frozen.cdf, alternative="two-sided"))
# KstestResult(statistic=0.019824350810698554, pvalue=0.8191867386190135)一点注意ですが、どのような仮説検定でもそうである通り、帰無仮説が棄却されなかったからと言って正しいことが証明されたわけではありません。(帰無仮説は採択されない。)
さて、scipyで実行してみて、この検定が使えるようになったのですが、より理解を深めるために、自分で統計量を計算してみようと思います。
KS検定の統計量の計算には、経験分布というものを使います。要するに標本から作成した累積分布関数ですね。数式として書くと標本$y_1, y_2,\dots, y_n$に対する経験分布$F_n$は次のようになります。
$$F_n(x) = \frac{\#\{1\le i\le n | y_i \le n\}}{n}$$
要するに$x$以下の標本を数えて標本のサイズ$n$で割ってるだけです。
そして、検定したい分布の分布関数$F$とこの$F_n$に対して、KS検定の統計量は次のように計算されます。
$$\begin{align}
max(最大値)ではなく、sup(上限)で定義されているのがポイントですね。
この$D_n$の直感的なイメージを説明すると、$F$と$F_n$の差が一番大きくなるところの値を取ってくることになるでしょうか。
経験分布の方を実装して可視化してみます。
# 経験分布関数
def empirical_distribution(x, samples):
return len([y for y in samples if y <= x])/len(samples)
xticks_2 = np.linspace(-40, 60, 100001) # メモリを細かめに取る
# 経験分布関数の値
empirical_cdf = np.array([empirical_distribution(x, t_samples) for x in xticks_2])
# 可視化
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(1, 1, 1)
ax.plot(xticks_2, norm_frozen.cdf(xticks_2), label="正規分布")
ax.plot(xticks_2, empirical_cdf, label="経験分布")
ax.legend()
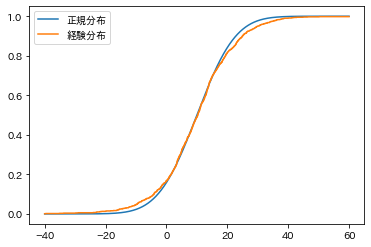
plt.show()出てきた図がこちらです。標本サイズが大きいのでよくみないとわかりませんが、オレンジの方は階段状の関数になっています。
この、青線(検定する正規分布)とオレンジの線(標本からの経験分布)が一番離れたところの差を統計量にしましょう、というのが考え方です。
では$D^+_n$から計算しましょう。実は(今回の例では)青線が滑らかなのに対して、オレンジの線が階段状になっているので、この段が上がるポイント、つまり標本が存在した点での値だけ調べると$D^+_n$が計算できます。
dplus = max([empirical_distribution(x, t_samples) - norm_frozen.cdf(x) for x in t_samples])
print(dplus)
# 0.031236203108694176次に$D^-_n$の方ですが、これは少し厄介です。サンプルが存在する点ではなく、その近傍を調べて階段の根元の値と累積分布関数の差を取りたいんですよね(ここでmaxではくsupが採用されていた意味が出てくる)。1e-10くらいの極小の定数を使って計算することも考えましたが、経験分布関数の方を少しいじって計算してみることにしました。どういうことかというと、x以下の要素の割合ではなくx未満の要素の割合を返すようにします。これを使うとサンプルが存在した点については階段の根元の値が取れるようになるので、これを使って$D^+_n$と同様に計算してみます。
def empirical_distribution_2(x, samples):
return len([y for y in samples if y < x])/len(samples)
dminus = max([norm_frozen.cdf(x) - empirical_distribution_2(x, t_samples) for x in t_samples])
print(dminus)
# 0.04361195130340301さて、必要だった統計量は$D^+_n$,$D^-_n$の最大値です。これをライブラリが計算してくれた統計量と比較してみましょう。一致しますね。
print("自分で計算したKS値:", max([dplus, dminus]))
# 自分で計算したKS値: 0.04361195130340301
print("scipyのKS値:", ks_vakue)
# scipyのKS値: 0.04361195130340301さて、統計量がわかったら次はp値を計算します。ウィキペディア を見ると、この統計量は無限和を含むそこそこ厄介な確率分布に従うことが知られているそうです。
非常にありがたいことに、kstwo とksone という両側検定、片側検定に対応してそれぞれ分布関数を用意してくれています。
統計量は求まっていますし、分布関数もあるのでp値はすぐ出せます。
print(kstwo.sf(max([dplus, dminus]), n=1000))
# 0.04325168699194537
# 参考 kstestから取得したp値
print(p_value)
# 0.04325168699194537最後、少し妥協しましたが、追々kstwo分布についても自分でスクラッチ実装して検証しておこうと思います。
今回の検証でコルモゴロフ–スミルノフ検定についてだいぶ理解が深まったので、これからバシバシ使っていこうと思います。
1標本だけでなく2標本でそれぞれの分布が等しいかどうかを検定するって使い方もできるので、次の記事はそれを取り上げようかなと思っています。