前回に続いて、statsmodelsの季節分解の話です。
参考(前回の記事): statsmodelsを利用した時系列データの季節分解のやり方
前回の記事は使い方でしたが、今回はソースコードを参照しながらどのような計算方法で季節分解が実装されているのかを見ていきます。
ちなみに、僕の環境のバージョンは以下の通りです。将来のバージョンでは仕様が変わる可能性もあるのでご注意ください。
$ pip freeze | grep statsmodels
> statsmodels==0.13.2
ドキュメントにソースコードが載ってるページがあるので、そこを参照します。
ソース: statsmodels.tsa.seasonal — statsmodels
ソースの先頭に以下のようにコメントが書かれている通り、移動平均を使って実装されています。
"""
Seasonal Decomposition by Moving Averages
"""
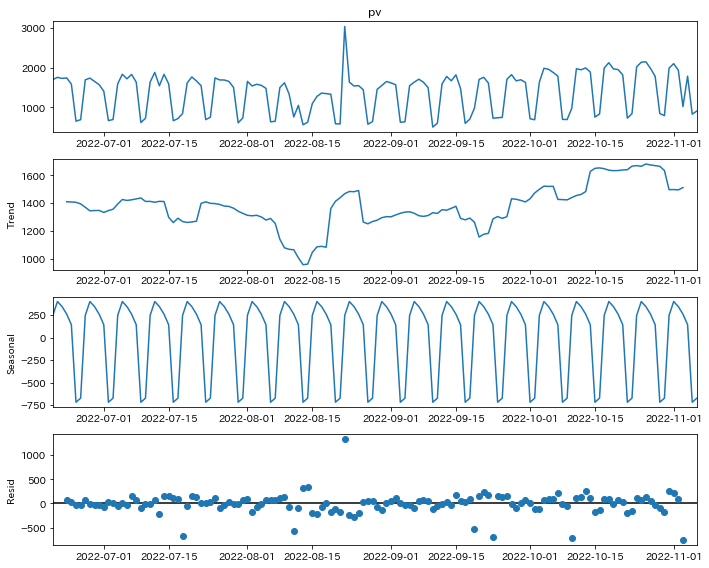
利用するデータですが、前回の記事と同じ、このブログのPVです。
# データ件数
print(len(df))
# 140
# 2週間分のデータ
print(df.tail(14))
"""
pv
date
2022-10-24 2022
2022-10-25 2140
2022-10-26 2150
2022-10-27 1983
2022-10-28 1783
2022-10-29 847
2022-10-30 793
2022-10-31 1991
2022-11-01 2104
2022-11-02 1939
2022-11-03 1022
2022-11-04 1788
2022-11-05 830
2022-11-06 910
"""
それでは順番にやっていきましょう。モデルは加法モデルの方を取り上げます。乗法モデルもトレンド成分を抽出するところまでは一致していますし、その後の処理から異なりますが加法と乗法の違いを考えれば普通に理解できると思います。
そして、ここが重要なのですが、まず周期が奇数の場合を見ていきます。今回は1週間である7日です。なんでこれが重要かというと、偶数の場合は少し挙動が特殊だからです。
季節分解では、元の時系列データからトレンド成分と季節成分を取り出します(残りが残差)が、処理の順番もこの順番になっていて、最初にトレンド成分、次に季節成分を取り出すようになっています。これ順番逆にすると結果変わりますし、それぞれメリットデメリットあるのですがトレンド成分を先にFIXすることを選ばれているようです。
では、トレンド成分の抽出を見ていきましょう。これ、”by Moving Averages”のコメント通り、移動平均です。two_sided=True (デフォルト)の設定場の場合、その対象日を挟むようにして、前後の期間から取った移動平均をその日のトレンド成分の値とします。
7日だったら、3日前,2日前,1日前,当日,1日後,2日後,3日後 の平均を使います。
pandasで計算するなら、rolling()で移動平均取って、shift()でずらすと同じ値が得られます。
モデルで取り出したトレンド成分と、pandasで自分で計算した値見てみましょう。
# モデルで計算
from statsmodels import api as sm
decompose_result = sm.tsa.seasonal_decompose(
df["pv"],
period=7,
)
print(decompose_result.trend)
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 1409.857143
2022-06-24 1408.714286
...
2022-11-02 1495.285714
2022-11-03 1512.000000
2022-11-04 NaN
2022-11-05 NaN
2022-11-06 NaN
Name: trend, Length: 140, dtype: float64
"""
# pandasで計算。7日移動平均をとって、3日シフトする
print(df["pv"].rolling(7).mean().shift(-3))
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 1409.857143
2022-06-24 1408.714286
...
2022-11-02 1495.285714
2022-11-03 1512.000000
2022-11-04 NaN
2022-11-05 NaN
2022-11-06 NaN
Name: pv, Length: 140, dtype: float64
"""
データの大部分…て略されてますが、これらは一致します。(極小値の誤差はあり得ますが)
two_sided = False とすると、前後のデータではなくその日含めた過去のデータだけ使われるようになるので、6日前〜当日のデータでの移動平均になります。
比較できるように、最初の2個の値が見れるようにprintしました。先頭のNaNの数が6個になってますね。表示てませんが、代わりに末尾のNaNは無くなります。
decompose_result = sm.tsa.seasonal_decompose(
df["pv"],
period=7,
two_sided=False
)
print(decompose_result.trend.iloc[: 8])
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 NaN
2022-06-24 NaN
2022-06-25 NaN
2022-06-26 1409.857143
2022-06-27 1408.714286
Name: trend, dtype: float64
"""
さて、トレンド成分の計算方法はわかったので、季節成分の話に戻ります。モデルも two_sided=Trueの最初の例の方に話戻してこちらで進めます。(この記事真似して再現する人は上のtwo_sided=Falseのコードブロックをスキップして実行してください)
季節成分は、トレンド成分を取り除き終わったデータから計算します。(最初と最後の数件のデータはNaNになっているのでこれらは使いません。)
説明が難しいのですが、今回みたいに曜日ごとの周期であれば、月曜の平均、火曜の平均、水曜の平均と、周期分の平均値を取り出し、さらにこうして計算した平均値たちからその平均を引いて標準化します。
言葉で書くとわかりにくいのでコードでやってみます。
import numpy as np
# 先述のトレンド成分の計算
df["pv_trend"] = df["pv"].rolling(7).mean().shift(-3)
# トレンド成分を取り除く
df["pv_detrended"] = df["pv"] - df["pv_trend"]
# 曜日ごとの平均を取る
period_averages = np.array([df["pv_detrended"][i::7].mean() for i in range(7)])
print(period_averages)
"""
[ 243.2556391 397.69172932 341.57894737 257.54285714 139.98496241
-720.2481203 -675.17293233]
"""
# 曜日ごとの平均から、さらにそれらの平均を引く
period_averages -= period_averages.mean()
print(period_averages)
"""
[ 245.450913 399.88700322 343.77422127 259.73813104 142.18023631
-718.0528464 -672.97765843]
"""
# 比較用。statsmodelsが算出した季節成分
decompose_result = sm.tsa.seasonal_decompose(
df["pv"],
period=7,
)
print(decompose_result.seasonal[: 7])
"""
date
2022-06-20 245.450913
2022-06-21 399.887003
2022-06-22 343.774221
2022-06-23 259.738131
2022-06-24 142.180236
2022-06-25 -718.052846
2022-06-26 -672.977658
Name: seasonal, dtype: float64
"""
データの形式が違いますが、モデルの結果と値が一致してるのがわかりますね。
以上で、トレンド成分と季節成分が計算できました。あと、statsmodelsは残差を計算できますがこれは単にトレンド成分と周期成分を元のデータから取り除いてるだけです。 df[“pv_detrended”] はトレンド成分除去済みなのでここから季節成分も引いてみます。
# np.tile で同じ値を繰り返す配列を作って引く
print(df["pv_detrended"] - np.tile(period_averages, 20))
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 74.404726
2022-06-24 36.105478
...
2022-11-02 99.940064
2022-11-03 -749.738131
2022-11-04 NaN
2022-11-05 NaN
2022-11-06 NaN
Name: pv_detrended, Length: 140, dtype: float64
"""
# モデルの残差
print(decompose_result.resid)
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 74.404726
2022-06-24 36.105478
...
2022-11-02 99.940064
2022-11-03 -749.738131
2022-11-04 NaN
2022-11-05 NaN
2022-11-06 NaN
Name: resid, Length: 140, dtype: float64
"""
以上が、statsmodelsにおける seasonal_decompose の実装の説明になります。
さて、ここからはちょっと補足で、周期が偶数の場合の挙動になります。月次データだと12を使うことが多いので周期が偶数というのはよくあるケースです。
説明をコンパクトにするために、周期(period=)4を例に取り上げます。
周期7の時、3日前から3日後までのデータの平均でトレンド成分を取り出してましたが、こういう期間の取り方ができるのは周期が奇数だったからで、偶数だとこうはいきません。
では、どうするのかというと、例えば周期が4日だったら、前日から翌日までの3日分のデータはそのまま使い、2日前と2日後のデータをそれぞれ0.5倍したものを計算に入れます。
# 周期4の場合のトレンド成分
decompose_result = sm.tsa.seasonal_decompose(
df["pv"],
period=4,
)
print(decompose_result.trend.iloc[: 5])
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 1719.750
2022-06-23 1567.250
2022-06-24 1299.125
Name: trend, dtype: float64
"""
# 以下、 2022-06-22 1719.750 が算出されるまでの計算式
# 元のデータ
df["pv"].iloc[: 5]
"""
date
2022-06-20 1703
2022-06-21 1758
2022-06-22 1732
2022-06-23 1744
2022-06-24 1587
Name: pv, dtype: int64
"""
# 計算 2日前〜2日後の5日分のデータから算出。ただし、最初と最後の日はウェイトが0.5
(1703*0.5 + 1758 + 1732 + 1744 + 1587*0.5)/4
# 1719.75
rolling()とshift()では同じ値を得られなかったので戸惑ったこともありましたが、まぁ、仕掛けがわかってしまえば簡単ですね。その日を挟んだ4日分のデータを考慮する手段としても一定の妥当性があると思います。
で、ここからが僕的には納得がいってないのですが、two_sided=Falseで周期を偶数(今の例では4)にした場合の挙動は少し不思議です。その日を含む過去4日分のデータを使えるので、単純に4日間の平均を取ればいいのに、そういう実装になっておらず、two_sided=Trueの場合の結果を単純にshiftしたものを使っています。要するに4日前の0.5倍と3日前から1日前、そして当日の0.5倍のデータを使ってます。two_sided=Falseにしたコードが以下ですが、上のTrue(省略した場合の値)と値が一致しているのがわかると思います。
decompose_result = sm.tsa.seasonal_decompose(
df["pv"],
period=4,
two_sided=False,
)
print(decompose_result.trend.iloc[: 7])
"""
date
2022-06-20 NaN
2022-06-21 NaN
2022-06-22 NaN
2022-06-23 NaN
2022-06-24 1719.750
2022-06-25 1567.250
2022-06-26 1299.125
Name: trend, dtype: float64
"""
ここの挙動だけは将来のバージョンで修正されるのではと思っているのですが、
一旦今はこういう作りになっているということを頭に置いた上で気をつけて使うしかないようです。