折れ線グラフや散布図に比べると利用頻度が落ちますが、
2次元から1次元への写像の可視化として等高線を使うことがあるので、そのメモです。
使う関数は、線を引く場合は、contour,色を塗る場合は contourf を使います。
サンプルの関数は何でもいいのですが、今回はこれを使います。
$$
1-\exp(-x^2+2xy-2y^2)
$$
まずはデータの準備です。
import matplotlib.pyplot as plt
import numpy as np
# 関数の定義
def f(x, y):
return 1- np.exp(-x**2 + 2*x*y - 2*y**2)
# プロットする範囲のmeshgridを作成する。
X = np.linspace(-2,2,41)
Y = np.linspace(-2,2,41)
xx, yy = np.meshgrid(X, Y)
そして可視化してみます。まずは等高線から。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.contour(xx,yy,f(xx, yy))
plt.show()

次に、色を塗る場合。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.contourf(xx,yy,f(xx, yy), alpha=0.5)
plt.show()
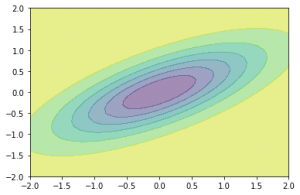
色の指定などをきちんとしていないのですが、まあまあみやすく可視化できていますね。
機械学習の決定境界の可視化などでも、これと同じ方法を使うことがあります。