statsmodels でカーネル密度推定

今回は statsmodelsを使ったカーネル密度推定を紹介します。

ドキュメントはこちらです: statsmodels.nonparametric.kde.KDEUnivariate

statsmodelsのいつもの作法で、インスタンスを作る時にデータを渡し、fitメソッドを呼び出せば完了です。
(SciPyではfitは必要なかったので注意)

fit する時に、カーネル関数の種類やバンド幅の決定方法を指定できます。
詳しくは fit メソッドのドキュメントを確認してください。

カーネル関数が 7種類指定できたり、バンド幅の指定方法が少し違ったりします。

ではやっていきましょう。比較のため、 SciPyで推定した結果も載せていきます。
(SciPyのバンド幅指定のルールがおかしいと言う話もあるので。参考記事はこちら。)
まずはデータ生成です。


import numpy as np
import statsmodels.api  as sm
import matplotlib.pyplot as plt
from scipy.stats import norm, gaussian_kde

# 推定したい分布の真の確率密度関数
def p_pdf(x):
    return (norm.pdf(x, loc=-4, scale=2)+norm.pdf(x, loc=2, scale=1))/2


# その分布からのサンプリング
def p_rvs(size=1):
    result = []
    for _ in range(size):
        if norm.rvs() < 0:
            result.append(norm.rvs(loc=-4, scale=2))
        else:
            result.append(norm.rvs(loc=2, scale=1))
    return np.array(result)


# グラフ描写のため真の確率密度関数の値を取得しておく
xticks = np.linspace(-10, 5, 151)
pdf_values = p_pdf(xticks)

# 100件のデータをサンプリング
data = p_rvs(100)

さて、ここから SciPyと statsmodelsでそれぞれのScottのルールとSilvermanのルールでカーネル密度推定して結果を可視化します。


# SciPyのカーネル密度推定
kde_scipy_scott = gaussian_kde(data, bw_method="scott")
kde_scipy_silverman = gaussian_kde(data, bw_method="silverman")

# statusmodels のカーネル密度推定
kde_sm_scott = sm.nonparametric.KDEUnivariate(data)
kde_sm_scott.fit(kernel="gau", bw="scott")
kde_sm_silverman = sm.nonparametric.KDEUnivariate(data)
kde_sm_silverman.fit(kernel="gau", bw="silverman")

fig = plt.figure(figsize=(7, 7), facecolor="w")
ax = fig.add_subplot(1, 1, 1, title="カーネル密度推定の結果")
ax.plot(xticks, pdf_values, label="真の分布")
ax.plot(xticks, kde_scipy_scott.evaluate(xticks), label="SciPy - Scott")
ax.plot(xticks, kde_scipy_silverman.evaluate(xticks), alpha=0.5, label="SciPy - Silverman")
ax.plot(xticks, kde_sm_scott.evaluate(xticks), linestyle=":", label="statsmodels - Scott")
ax.plot(xticks, kde_sm_silverman.evaluate(xticks), label="statsmodels - Silverman")
ax.hist(data, bins=20, alpha=0.1, density=True, label="標本")
ax.legend()
plt.show()

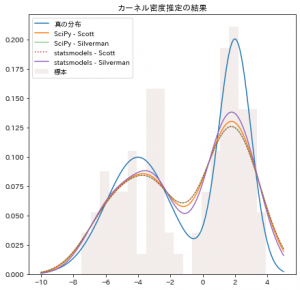
出力がこちらです。

statsmodels で Silverman のルールを使ったのが一番良さそうですね。
ただ、これは常にそうなるわkではなく、元の分布の形や標本サイズによって何が最適かは変わってきます。

SciPyのSilvermanのルールと、statsmodelsのScottのルールが重なってしまうのは、先日の記事で書いた通り、SciPyの不備と思われます。

さて、こうしてみると、 statsmodels が一番良さそうに見えますが、当然これにも欠点があります。
SciPyやscikit-learnのカーネル密度推定では多次元のデータも扱えるのですが、
statsmodelsでは1次元のデータしか扱えません。

カーネル密度推定に関しては SciPy, scikit-learn statusmodels　それぞれにメリットデメリットあるので、
目的に応じて使い分けていくのが良さそうです。
(これにそこまで高い精度が求められることも少ないので一番手軽に書ける SciPyで十分なことが多いと思います。)

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル