前回の記事でkerasを使えるようにしたので、
動作確認を兼ねて非常に単純なモデルを作ってみました。
線形分離可能なサンプルではつまらないので、半径の異なる2円のToyDataでやってみましょう。
scikit-learnにmake_circlesという関数があるので、これを使います。
早速データを生成して訓練データとテストデータに分け、訓練データの方を可視化してみます。
# 必要なモジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from keras.models import Sequential
from keras.layers.core import Dense
# データの準備
data, target = make_circles(n_samples=2000, noise=0.2, factor=0.3)
X_train, X_test, y_train, y_test = train_test_split(
data,
target,
test_size=0.2,
stratify=target
)
# 訓練データの可視化
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, aspect='equal', xlim=(-2, 2), ylim=(-2, 2))
ax.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], marker="o")
ax.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], marker="x")
plt.show()
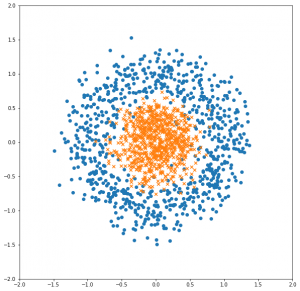
これが出力された散布図です。
一部ノイズはありますが概ね綺麗に別れていて、動作確認には手頃な問題になっていると思います。
早速ですが、kerasでモデルを作っていきます。
kerasのドキュメントはここです。日本語版があって便利ですね。
特に何も考えず、中間層が1層あるだけのシンプルなニューラルネットワークで作ります。
とりあえず動けば良いので、今回はDropoutもCallbackもなしで。
# モデルの構築
model = Sequential()
model.add(Dense(16, activation='tanh', input_shape=(2,)))
model.add(Dense(1, activation='sigmoid'))
model.summary()
model.compile(
optimizer='adam',
loss='binary_crossentropy',
metrics=['acc']
)
# 以下、出力
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 16) 48
_________________________________________________________________
dense_2 (Dense) (None, 1) 17
=================================================================
Total params: 65
Trainable params: 65
Non-trainable params: 0
_________________________________________________________________
モデルができたので、学習させます。
epochsもbatch_sizeも適当です。
# 学習
history = model.fit(
X_train,
y_train,
epochs=100,
batch_size=32,
validation_data=[X_test, y_test]
)
正常に学習が進んだことを確認するために、
損失関数と正解率の変動を可視化してみましょう。
# Epoch ごとの正解率と損失関数のプロット
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(2, 1, 1, title="loss")
ax.plot(history.epoch, history.history["loss"], label="train_loss")
ax.plot(history.epoch, history.history["val_loss"], linestyle="-.", label="val_loss")
ax.legend()
ax = fig.add_subplot(2, 1, 2, title="acc")
ax.plot(history.epoch, history.history["acc"], label="train_acc")
ax.plot(history.epoch, history.history["val_acc"], linestyle="-.", label="val_acc")
ax.legend()
plt.show()
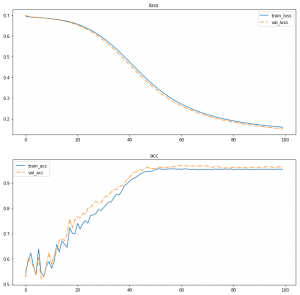
できたグラフがこちら。
順調に学習できていますね。
訓練データで評価してみましょう。
もともとやさしい問題なので、なかなかの正解率です。
print(classification_report(y_train, model.predict_classes(X_train)))
# 出力結果
precision recall f1-score support
0 0.95 0.96 0.95 800
1 0.96 0.95 0.95 800
avg / total 0.95 0.95 0.95 1600
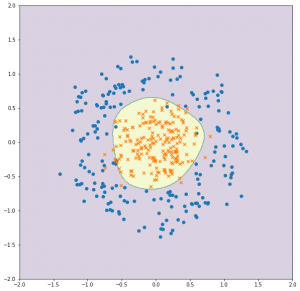
最後に、決定境界を可視化してみます。
以前紹介した、等高線のプロットを使います。
# 決定境界の可視化
X_mesh, Y_mesh = np.meshgrid(np.linspace(-2, 2, 401), np.linspace(-2, 2, 401))
Z_mesh = model.predict_classes(np.array([X_mesh.ravel(), Y_mesh.ravel()]).T)
Z_mesh = Z_mesh.reshape(X_mesh.shape)
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, aspect='equal', xlim=(-2, 2), ylim=(-2, 2))
ax.contourf(X_mesh, Y_mesh, Z_mesh, alpha=0.2)
plt.scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1], marker="o")
plt.scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1], marker="x")
plt.show()
出力がこちら。
真円にはなっていませんが、きちんと円の内側と外側にデータを分離できました。