昔、グラフ関係の記事を書いてた頃に書いてたと思ってたら、まだ書いてなかったので、グラフのコミュニティーを検出する方法を書きます。
グラフのコミュニティ検出というのは、グラフのノードを複数のグループに分け、同じグループ内のノード同士ではエッジが密で、異なるグループのノード間ではエッジが疎になる様にすることを言います。人の集まりを仲良しグループでいくつかの組に分けるのに似ていますね。この記事の最後にも結果の例の画像をつけていますのでそれをみていただくとイメージがつきやすいと思います。
複数のアルゴリズムが存在するのですが、僕が一番気に入っていてよく使っているのはLouvain法による方法なのでこれを紹介していきます。
参考: Louvain method – Wikipedia
このLouvain法では、グラフとコミュニティに対してモジュラリティ(modularity)という指標を定義し、このモジュラリティが最大になる様なコミュニティの分け方を探すことでグラフのノードを分割します。モジュラリティの定義式はWikipediaにもありますが以下の通りです。
$$Q=\frac{1}{2m}\sum_{ij}\left[A_{ij}\ -\ \frac{k_ik_j}{2m} \right]\delta(c_i, c_j).$$
ここで、各記号の意味は以下の通りです。
$A_{ij}$: ノード$i$, ノード$j$間のエッジの重み。
$k_i, k_j$: ノード$i$, ノード$j$それぞれに接続されたエッジの重みの合計。
$m$: グラフの全てのエッジの重みの合計。
$c_i, c_j$: ノード$i$, ノード$j$それぞれが所属しているコミュニティ。
$\delta$: クロネッカーのデルタ。二つの引数が等しければ1でそれ以外は0を返す関数。
元論文を読めていないのですが、ライブラリの挙動を確認した結果によると、和の$ij$は$i$, $j$の全てのペアを渡る和で$i,j$の組み合わせとそれを入れ替えた$j, i$の組み合わせを両方取り、さらに$i=j$となる自己ループなエッジも考慮している様です。
さて、実際にやってみましょう。Pythonでは、communityというライブラリがあり、Louvain法が実装されています。(networkx自体にも他のコミュニティ検出のアルゴリズムが実装されているのですが、Louvain法は別ライブラリになっています。)
pipyでの登録名がpython-louvainなので、インストール時のコマンドが以下であることに注意してください。Pythonでimportするときと名前が違います。
$ pip install python-louvainドキュメントはこちら
参考: Community detection for NetworkX’s documentation — Community detection for NetworkX 2 documentation
早速使ってみましょう。例としてコミュニティがわかりやすいグラフを乱数で生成します。
0~29のノードを持ち、0~9, 10~19, 20〜29が同じコミュニティで、同コミュニティー内では50%の確率でエッジが貼られていて異なるミュにティだと2%の確率でしかエッジがないという設置です。
import numpy as np
import networkx as nx
import community
# 30個のノード
node_list = list(range(30))
# 同じクラスタ内は0.5, 別クラスタは0.02の確率でエッジを生成する
edge_list = []
np.random.seed(1) # シード固定
for i in range(30):
for j in range(i+1, 30):
if i // 10 == j // 10:
if np.random.rand() < 0.5:
edge_list.append((i, j))
else:
if np.random.rand() < 0.02:
edge_list.append((i, j))
# グラフ生成
G = nx.Graph()
G.add_nodes_from(node_list)
G.add_edges_from(edge_list)さて、グラフができたのでコミュニティ検出をやっていきます。これものすごく簡単で、best_partitionというメソッドにnetworkxのグラフオブジェクトを渡すとノードと所属するグループの辞書として結果が帰ってきます。
注意点ですが、アルゴリズムの高速化のための工夫の弊害により絶対にベストな分割が得られるというわけではなく少々確率的な振る舞いをします。今回のサンプルコードでは非常にわかりやすい例を用意したので一発で成功していますが、通常の利用では何度か試して結果を比較してみるのが良いでしょう。
ではやっていきます。
partition = community.best_partition(G)
print(partition)
"""
{0: 2, 1: 2, 2: 2, 3: 2, 4: 2, 5: 2, 6: 2, 7: 2, 8: 2, 9: 2,
10: 0, 11: 0, 12: 0, 13: 0, 14: 0, 15: 0, 16: 0, 17: 0, 18: 0, 19: 0,
20: 1, 21: 1, 22: 1, 23: 1, 24: 1, 25: 1, 26: 1, 27: 1, 28: 1, 29: 1}
"""0〜9は2で、10〜19は0で、20〜29は1と、綺麗に分類できてますね。
画像に表示してみましょう。ドキュメントのサンプルコードだとlist(partition.values())と辞書の値をそのまま可視化メソッドに渡していますが、辞書型のデータなので順序は保証されておらずこれはリスキーな気がします。実はそれでもうまくいくのですが念のため、ノードと順番が揃う様に配列として取り出してそれを使う様にしました。
# ノードの並びと同じ順でグループのリストを配列として取得する。
partition_list = [partition[n] for n in G.nodes]
# 配置決め
pos = nx.spring_layout(G, seed=3)
# 描写
nx.draw_networkx(G, node_color=partition_list, cmap="tab10", pos=pos)結果がこちらです。
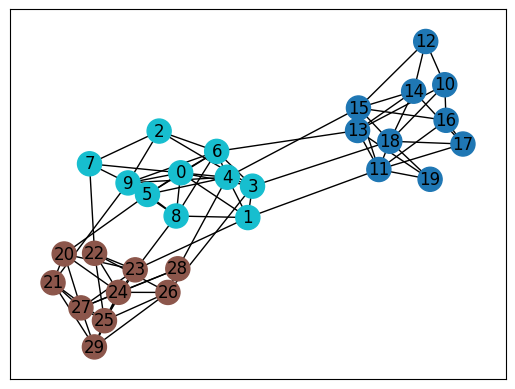
綺麗に3グループに分かれていますね。
ちなみに、このグループ分けのモジュラリティを取得するメソッドもあります。グループ分けとグラフ本体のデータをそれぞれ渡すことで使えます。
print(community.modularity(partition, G))
# 0.5316751700680272結構高いですね。