諸事情ありグラフが平面グラフかどうか手軽に判定する方法が必要になったので、その方法を調べました。(正確には、僕が調べたかったのは平面的グラフかどうかですが。)
平面グラフの定義についてはWikipediaがわかりやすいです。
参考: 平面グラフ – Wikipedia
簡単にいうと、グラフを2次元の図に可視化したときに、辺が交差しない様に書いたものが平面グラフです。そして、グラフによっては描き方によって辺が交差したりしなかったりするのですが、平面グラフと同型なグラフを平面的グラフと呼びます。
どうにか頑張れば辺が交差しない様に頂点を配置できるグラフが平面的グラフ、どうやってもどこかで交差してしまうグラフが平面的で無いグラフ、と考えた方がわかりやすいでしょう。
これをどうやって判定しようかなと考えていたのですが、networkxに専用のメソッドが用意されていました。
– check_planarity
– is_planar
is_planar の方がシンプルで、NetworkXのグラフオブジェクトを渡すとそれが平面的だったかどうかでTrue/Falseを返してくれます。
check_planarity の方は、平面的だったかどうかの情報だけでなく、埋め込みの情報も取得できます。これは、ノードをどの様に配置したら平面的になるかを示すものです。
is_planar の方が結果がシンプルなので速度面で早いとか何かメリットあるのかなと思っていたのですが、NetworkXのソースコードを見ると、内部でcheck_planarityを呼び出して、一個目の戻り値だけを返すという作りだったのでそういうメリットはなさそうです。
とりあえず、結果がシンプルなis_planarの方を使ってみます。
import networkx as nx
# 頂点4個の完全グラフは平面的
K4 = nx.complete_graph(4)
print(nx.is_planar(K4))
# True
# 頂点5個の完全グラフは平面的では無い
K5 = nx.complete_graph(5)
print(nx.is_planar(K5))
# False簡単ですね。
check_planarityの方を使う場合は、戻り値として判定結果と埋め込み情報が返ってくるので、それぞれ個別に受け取ります。
is_planar, P = nx.check_planarity(K4)
print(is_planar)
# True
print(P)
# PlanarEmbedding with 4 nodes and 12 edges
# これは、ノードをキーにして辞書の様にして使うと中身を見れる。
print(P[0])
# {1: {'cw': 3, 'ccw': 2}, 2: {'cw': 1, 'ccw': 3}, 3: {'cw': 2, 'ccw': 1}}
# 上記の結果で、ノード0に、1, 2, 3と繋がるエッジがあることがわかる。
print(P[0][1])
# {'cw': 3, 'ccw': 2}
# これは、ノード0に他のノードがどの様な順番で繋がっているかを示し、
# ノード1の時計回りの隣が3,反時計回りの隣が2であることを示す。注意しないといけないのは、平面的グラフだからといって描写したら平面グラフで描かれるとは限らないという点です。というか、平面グラフで描かれる方が稀です。さっきの例で挙げた頂点4個の完全フラフでさえ、普通に力学モデルで配置したらエッジが交差します。
そのため、NetworkXでは平面グラフ描写用のメソッドも持っています。
参考: planar_layout — NetworkX 3.1 documentation
spring_layoutと比較してみましょう。なぜか、with_labels引数のデフォルト値が違うのでTrueつけないとノードのidを表示してくれません。
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12, 6), facecolor="w")
ax = fig.add_subplot(121, title="spring_layout")
ax.axis("off")
nx.draw_networkx(K4, ax=ax)
ax = fig.add_subplot(122, title="planar_layout")
nx.draw_planar(K4, ax=ax, with_labels=True)出てくる図がこちら。
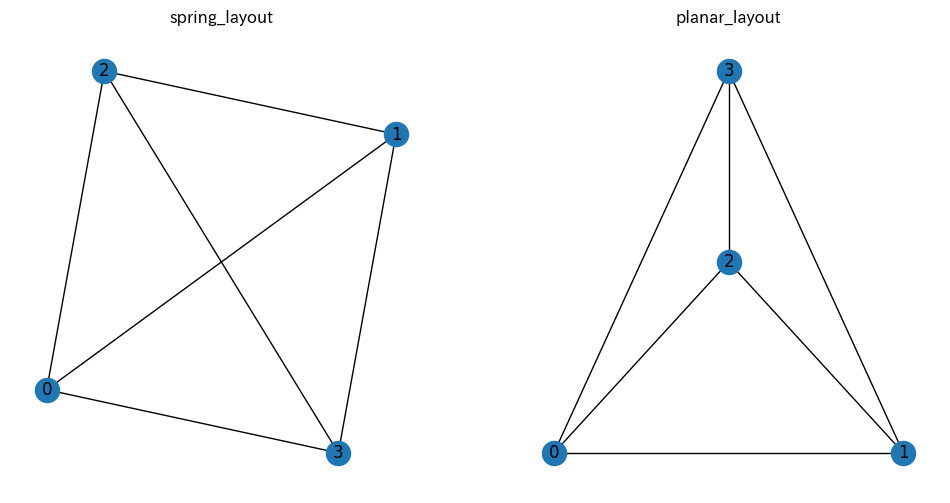
draw_planar を使わなくても、他のアルゴリズム同様にlayout系のメソッドで座標を取得してそれで描写することもできます。
参考: planar_layout — NetworkX 3.1 documentation
pos = nx.layout.planar_layout(K4)
print(pos)
"""
{0: array([-1. , -0.375]),
1: array([ 1. , -0.375]),
2: array([0. , 0.125]),
3: array([0. , 0.625])}
"""
nx.draw_networkx(K4, pos=pos)
# 結果略