今回は移動平均過程の例をいくつか生成して紹介します。
$AR(1)$や$AR(2)$の例は色々なところで取り上げられているので、すべて$AR(3)$にしました。
AR特性方程式の解の絶対値が全て1より大きい定常な例を一つと、そうではない例が3つです。
定常ではない例は、AR特性方程式の解に絶対値が$1$より小さなものを含むものと、
$-1$を解に持つもの、$1$を解に持つものを選びました。
なお、撹乱項の分散は$1$に揃えています。
$$\varepsilon_t \sim iid N(0,1)$$
定常なAR(3)過程の例
まずは、次のAR(3)過程を取り扱います。
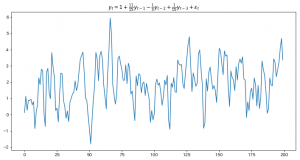
$$y_t=1+\frac{11}{15}y_{t-1}-\frac{1}{3}y_{t-2}+\frac{1}{15}y_{t-3}+\varepsilon_t$$
AR特性方程式の解は $3,1+2i,1-2i$の3個です。(意図的に虚数解を含むものを選びました。)
解の絶対値が全部1より大きいので、この過程は定常になるはずです。
pythonで時系列データを生成しプロットして見ます。
import sympy
import numpy as np
import matplotlib.pyplot as plt
phi_1 = 11/15
phi_2 = -1/3
phi_3 = 1/15
# 根の確認
z = sympy.symbols('z')
print(sympy.solve(1-phi_1*z-phi_2*z**2-phi_3*z**3))
# 過程の生成
y = np.zeros(200)
# 初期値
y[0] = np.random.randn()
y[1] = np.random.randn()
y[2] = np.random.randn()
for i in range(3, 200):
y[i] = 1 + phi_1*y[i-1] + phi_2*y[i-2] + phi_3*y[i-3] + np.random.randn()
fig = plt.figure(figsize=(12, 6))
title = '$y_t=1+\\frac{11}{15}y_{t-1}-\\frac{1}{3}y_{t-2}+\\frac{1}{15}y_{t-3}+\\varepsilon_t$'
ax = fig.add_subplot(1, 1, 1, title=title)
ax.plot(y)
plt.show()
いかにも定常な感じですね。
定常ではないAR(3)過程の例 1
次は定常ではないAR(3)過程の例としてこれを考えます。
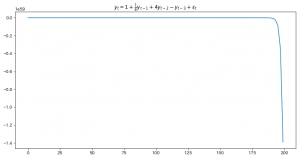
$$y_t=1+\frac{1}{4}y_{t-1}+4y_{t-2}-y_{t-3}+\varepsilon_t$$
AR特性方程式の解は $-0.5,0.5,4$ であり、絶対値が1より小さいものを含みます。
コードは省略しますが、試しに出力したのがこちら。
撹乱項の値によって形が全然変わるので実行するたびに プラスに振れるのかマイナスに振れるのかも違います。
どう見ても定常ではありませんね。$t$が小さい時と大きい時の$y_t$の期待値が全く違います。
定常ではないAR(3)過程の例 2
もう一つ定常ではないAR(3)過程の例。
今度はAR特性方程式が$-1$を解に持ちます。
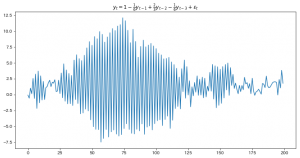
$$y_t=1-\frac{1}{6}y_{t-1}+\frac{2}{3}y_{t-2}-\frac{1}{6}y_{t-3}+\varepsilon_t$$
一見定常っぽくも見えますが、非常にギザギザしています。
実はこの過程、奇数番目と偶数番目の項の期待値が違います。
(撹乱項を取り払うと2つの値が交互に現れるので確認しやすいです)
このため、たしかに定常でないことがわかりました。
定常ではないAR(3)過程の例 3
次も定常ではない例ですが、今回はAR特性方程式が、$1$を解に持ちます。
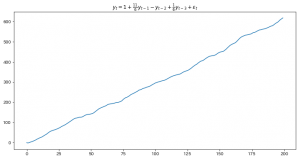
$$y_t=1+\frac{11}{6}y_{t-1}-y_{t-2}+\frac{1}{6}y_{t-3}+\varepsilon_t$$
実はこの過程は定常ではないのですが、差分系列$\Delta y_t=y_t-y_{t-1}$は定常過程になります。
このような過程を単位根過程と言います。
単位根過程の詳しい話はそのうち紹介したいですがとりあえずグラフを出すと次のようになります。
綺麗なトレンドが出ましたね。