このブログでもよく形態素解析ソフトのMeCabを利用していますが、今回の記事ではこのMeCabがどのようにして形態素解析を実現しているのかを紹介します。
ざくっと言うと、MeCabはあらかじめ辞書で定義された単語の情報をもとに、その単語の発生しにくさを示す「生起コスト」とそれぞれの単語間の繋がりにくさを示す「連接コスト」を計算し、これらの合計が最小になるように文を分割します。
辞書にない単語(未知語)がある場合はその部分についてまた別のロジックが実装されているのですが、今回はこの生起コストと連接コストの概念について説明するために辞書にある単語だけでできている文をサンプルに使います。使うのは定番の「すもももももももものうち」です。
実際のMeCabには速度改善のための工夫なども取り込まれていて、実際にこの記事の通りに実装されているわけではないのですが、大まかな流れはおそらくあってると思います。
それでは早速やっていきましょう。
最初にMeCabが行うのは文をくぎれる位置で全部区切り、辞書にある単語を洗い出します。
i と j を順番に動かして、元の文のi文字目からj文字目までを全部取るような処理なので比較的簡単ですね。例えば、元の文が「すもも」だけであれば、す/すも/すもも/も/もも などが候補になり、これらを全部辞書の中から探します。「すもももももももものうち」だと、78通りも切り出せる単語があり大変です。MeCabでは「すももも」ではじまる単語がないことを検知すると、「すもももも」以降は試さないなどの工夫がされているそうです。
文から取り出した単語の一覧ができたら、それらを辞書と付き合わせます。表記が同じでも違う品詞の組み合わせなども非常に多くあります。
IPA辞書の場合、「すもももももももものうち」から切り出せる文字列のうち、
[‘う’, ‘うち’, ‘す’, ‘すも’, ‘すもも’, ‘ち’, ‘の’, ‘のう’, ‘も’, ‘もの’, ‘ものう’, ‘もも’]
の13語が辞書に含まれていますが、「す」は7単語、「うち」は6単語も登録されています。
す,1285,1285,10036,名詞,一般,*,*,*,*,す,ス,ス
す,11,11,9609,形容詞,自立,*,*,形容詞・アウオ段,ガル接続,すい,ス,ス
す,879,879,11484,動詞,接尾,*,*,五段・サ行,基本形,す,ス,ス
す,777,777,9683,動詞,自立,*,*,五段・ラ行,体言接続特殊2,する,ス,ス
す,602,602,9683,動詞,自立,*,*,サ変・スル,文語基本形,する,ス,ス
す,601,601,9683,動詞,自立,*,*,サ変・スル,体言接続特殊2,する,ス,ス
す,560,560,10247,接頭詞,名詞接続,*,*,*,*,す,ス,ス
うち,1285,1285,7990,名詞,一般,*,*,*,*,うち,ウチ,ウチ
うち,1313,1313,5796,名詞,非自立,副詞可能,*,*,*,うち,ウチ,ウチ
うち,1310,1310,8911,名詞,非自立,一般,*,*,*,うち,ウチ,ウチ
うち,743,743,10640,動詞,自立,*,*,五段・タ行,連用形,うつ,ウチ,ウチ
うち,1306,1306,11865,名詞,代名詞,一般,*,*,*,うち,ウチ,ウチ
うち,1314,1314,8571,名詞,副詞可能,*,*,*,*,うち,ウチ,ウチ
さて、辞書を引いたら、元の文章におけるその文字列の登場位置と文字数を考慮し、どのような結合がありうるのかを列挙し、グラフにします。ここで言うグラフとは折れ線グラフや棒グラフではなく、ノードやエッジがあるグラフ理論のグラフの方です。要するに、「すもも」と「うち」は両方文中に登場しますが登場位置が離れているのでつながったりしないのです。
イメージとしては、次の図のようなグラフが生成されます。
あくまでもイメージです。下の図では、品詞など無視して、表層形が同じ単語を区別せずに描いています。実際は上で見た通り、同じ表層型でも異なる単語が多く存在するので実際にMeCab内部で処理されるグラフ(これをラティスというそうです)は遥かに複雑になります。
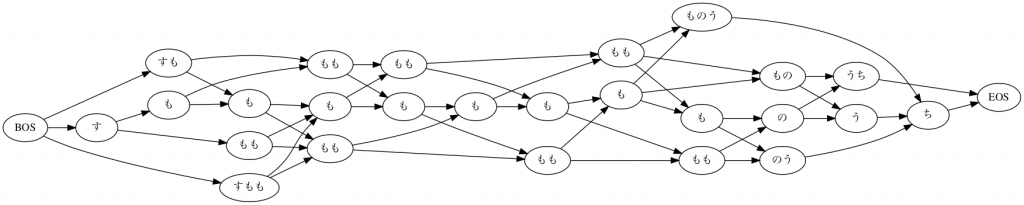
さて、ここまでで、元の文をどのように分解するのかの候補が出揃いました。あとはこれらの分解の候補の中から、最終的な形態素解析結果を決める必要があります。
そこで用いられる情報の一つが「生起コスト」です。これは辞書で各単語ごとに指定されていおり、その単語の文中での「表れにくさ」を示しています。つまり数値が小さいほど出現しやすいということです。
例えば、ももであれば一般名詞のももと、動詞もむが活用したももがあり得ますが、一般名詞のももの方がコストが低く設定されています。
もも,1285,1285,7219,名詞,一般,*,*,*,*,もも,モモ,モモ
もも,763,763,9357,動詞,自立,*,*,五段・マ行,未然ウ接続,もむ,モモ,モモわかりにくいですが、
表層形,左文脈ID,右文脈ID,コスト,品詞,品詞細分類1,品詞細分類2,品詞細分類3,活用型,活用形,原形,読み,発音
の順に並んでおり、4列目の 7219や9357がその単語の生起コストです。
一見すると、この生起コストだけでも形態素解析ができそうな気がしてきますね。
しかし、実際は単語の特定はその単語の出現しやすさだけでできるものではありません。
例えば、もし生起コストだけで形態素解析を行おうとすれば、名詞のももが動詞のもむが活用したももより出やすいという判断のもと、どんな文脈であってもももが出てきたら名詞(果物の)ももと判断してしまうことになり、これはおかしいです。
また、「すももももも」という文を考えると、生起コストだけでは「すもも/も/もも」なのか「すもも/もも/もも」なのか判断することができません。
これらの問題を解決するために、MeCabでは「連接コスト」という概念が導入されています。これは、品詞(と活用系)の組み合わせごとに、その「繋がりにくさ」を指定したものです。そのため、生起コスト同様に数値が低い方がよく現れやすいものとして扱われます。
連接コストは、辞書の matrix.def というファイルに入っています。辞書ディレクトリのmatrix.binはコンパイルされてバイナリになっちゃってますので、中身を確認したい場合は、コンパイル前のファイルを見てください。
中身はこんな感じです。
$ head matrix.def
1316 1316
0 0 -434
0 1 1
0 2 -1630
0 3 -1671一番上の 1316 1316 はヘッダーみたいなのもので、おそらく品詞の種類数を意味してると思います。2行目からがデータで、(おそらくですが、)左の単語の右文脈ID、右の単語の左文脈ID、連接コスト、と入っています。 0 は BOS/EOS の文脈IDで、これによって文頭や文末にきやすい品詞なども定義されています。
文脈IDと品詞の情報は、left-id.def / right-id.def に入っています。(両ファイルの中身は同じです。)
$ head left-id.def
0 BOS/EOS,*,*,*,*,*,BOS/EOS
1 その他,間投,*,*,*,*,*
2 フィラー,*,*,*,*,*,*
3 感動詞,*,*,*,*,*,*
4 記号,アルファベット,*,*,*,*,*
5 記号,一般,*,*,*,*,*
6 記号,括弧開,*,*,*,*,BOS/EOS
7 記号,括弧閉,*,*,*,*,BOS/EOS
8 記号,句点,*,*,*,*,BOS/EOS
9 記号,空白,*,*,*,*,*動詞は活用系も全部入ってるので、1316種類も品詞があります。そして、全ての組み合わせに対して、連接コストが定義されているので、matrix.def は 100万行を超えるファイルになっています。
例えば「名詞,一般のすもも」と、「助詞,係助詞のも」の連接コストは次のようにか確認できます。まずそれぞれの文脈IDを確認します。
すもも,1285,1285,7546,名詞,一般,*,*,*,*,すもも,スモモ,スモモ
も,262,262,4669,助詞,係助詞,*,*,*,*,も,モ,モ1285と262ですね。matrix.def で探すと、「1285 262 -4158」と出てきます。コストがマイナスですからこれらは非常に連接しやすいということがわかります。
先ほど例に挙げた「すももももも」の2通りの分解について生起コストと連接コストをグラフにまとめたのが次の図です。ノード中の数字が生起コスト、エッジのラベルが連接コストです。
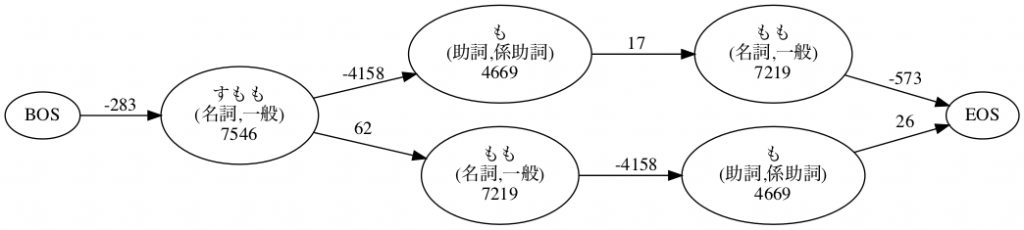
これを見ると、「すもも/も/もも」 の方が、合計14437(=-283+7546-4158+4669+17+7219-573)でコストが小さいことがわかります。ちなみに「すもも/もも/も」のコストは14721(=-283+7546+62+7219-4518+4669+26) です。
「すもももももももものうち」のラティスの方にこの連接コストのラベルまで書き込むと非常にごちゃごちゃする(そもそも上の図は品詞で区別してないので、連接コストを書き込むには品詞ごとにノードを分ける必要もある)ので、図は掲載しませんが、MeCabの内部では、ありうる全ルートの中から最もコストが小さくなるパスを探索して、形態素解析結果として出してくれています。
以上のようにして、MeCabでは形態素解析を実現しています。MeCab本体には日本語の文法などの情報は定義されていないそうで、あくまでも辞書によって定義された2種類のコスト情報だけでこれほどの精度の形態素解析を実現しているというのはすごいですね。