NumPyで多項式回帰

前回の記事で、NumPyの多項式オブジェクトを紹介したので、ついでに多項式回帰を行う方法を紹介したいと思います。
1変数の多項式回帰に関してはscikit-learnを使うよりもNumPyの方が手軽なのでおすすめです。

使うのは、 numpy.polyfit というメソッドです。
これの引数に、回帰したいデータセットのx座標とy座標をそれぞれリストで渡し、3つ目の引数で回帰する次元を渡すだけです。
戻り値は回帰した結果の係数が配列で得られます。

import numpy as np

# 真の関数
f = np.poly1d([2/9, -3, 9, 0])

# ノイズを加えて10点サンプルを取得する
x_sample = np.array(range(10))
np.random.seed(1)
y_sample = f(x_sample) + np.random.randn(10)

# 3次多項式で回帰した係数を取得する
c = np.polyfit(x_sample, y_sample, 3)
print(c)
# [ 0.19640272 -2.60339584  7.33961579  1.29981883]

簡単ですね。

この戻り値ですが、高次の項の係数から順番に格納されており、前回の記事で紹介した多項式オブジェクトを作成するnumpy.poly1dの引数としてそのまま渡すことができます。
とても便利です。

これを使って、回帰した多項式も含めてグラフにプロットしてみます。
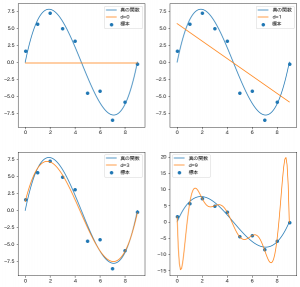
機械学習のテキストによくある、次数が低くて学習できてないパターンと、高くて過学習してるパターンを出してみました。

import matplotlib.pyplot as plt

# プロット用のxメモリ
x = np.linspace(-0, 9, 101)
y = f(x)
fig = plt.figure(figsize=(10, 10), facecolor="w")

for i, d in enumerate([0, 1, 3, 9], 1):
    # d次関数で回帰した係数
    c = np.polyfit(x_sample, y_sample, d)
    # d次関数オブジェクトに変換
    g = np.poly1d(c)
    ax = fig.add_subplot(2, 2, i)
    ax.plot(x, y, label="真の関数")
    ax.plot(x, g(x), label=f"d={d}")
    ax.scatter(x_sample, y_sample, label="標本")
    ax.legend()

plt.show()

出力がこちら。

どこかでみたことあるような図がバッチリ出ました。
真の関数の次数である3が一番もっともらしくフィットしていますね。