データから、そのデータを生成した背景にある確率分布を推定したいことはよくあります。
正規分布やポアソン分布を仮定するのであれば、簡単ですが、多くの分布では結構面倒です。
そこで、scipyのstatsにある、fitとという便利な関数を使って最尤推定します。
今回はベータ分布を例に取り上げます。
公式ドキュメントはここです。
scipy.stats.rv_continuous.fit
ここ、ベータ関数を使ったサンプルも乗ってるんですよね。
初めて読んだ時はもっと早く読めばよかったと思いました。
それでは、真の分布を設定して、そこからデータを生成し、パラメーターを推定してみます。
# モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# これから推定したい真の分布
frozen_beta_true = beta.freeze(a=3, b=7, loc=-2, scale=4)
# 真の分布に従うデータを生成
data = frozen_beta_true.rvs(500)
# データから最尤推定 (全パラメーター)
fit_parameter = beta.fit(data)
print(fit_parameter)
# 出力
# (2.548987294857196, 4.380552639785355, -1.946453704152459, 3.1301112690818194)
bの値と、scaleがちょっと乖離が大きいかなと感じられるのですが、
結構妥当な値が推定できました。
経験上、ベータ分布を使いたい時は、取りうる値の範囲が決まっていることが多いです。
そのため、locやscaleは固定して推定を行いたいのですが、
その時は、パラメーターにfをつけて、fitに渡すと、
それらのパラメーターは固定した上で残りを推定してくれます。
# データから最尤推定 (loc と scaleは指定する)
fit_parameter = beta.fit(data, floc=-2, fscale=4)
print(fit_parameter)
# 出力
# (3.1998198349509672, 7.4425425953673505, -2, 4)
かなり真の値に近い結果が出ました。
最後に推定した確率分布の確率密度関数を可視化してみましょう。
# 推定したパラメーターで確率分布を生成
frozen_beta = beta.freeze(*fit_parameter)
# 可視化
plt.rcParams["font.size"] = 14
x = np.linspace(-2, 2, 51)
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(1, 1, 1, xlim=(-2, 2), title="scipyによる最尤推定")
ax.plot(x, frozen_beta_true.pdf(x), label="真の分布")
ax.plot(x, frozen_beta.pdf(x), label="推定した分布")
ax.hist(data, bins=30, alpha=0.7, density=True, label="サンプルデータの分布")
ax.legend()
plt.show()
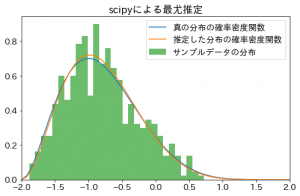
出力されたのがこちらの図です。
うまく推定されているように見えますね。
pythonを触り始めたばかりの頃は、scipyをうまく使えず、
確率分布はnumpyでスクラッチで書いて、この種の推定もゴリゴリ自分で実装していました。
(かなり効率の悪いアルゴリズムで)
fitを知ってからも、しばらくは4つの戻り値のどれがaでどれがlocなのかよくわからなかったり、
locやscaleを固定する方法を知らず長いこと敬遠していたのですが、
ちゃんとドキュメントを読めば全部書いてあるものです。