前回の記事で、正規分布に従う確率変数の母平均の区間推定を行う式を紹介しました。
参考:母平均の区間推定
これで、実際に信頼区間を計算すると、結構広い区間が求まります。
特にサンプルサイズが30とか50の時は、もっと絞り込めるんじゃないか?と感じる結果になることが多いです。
ぶっちゃけた話、95%信頼区間に99%くらいの確率で母平均が含まれてそうに見えます。
ということで、既知の分布から繰り返し標本を抽出し95%信頼区間を計算して、
その中に母平均が含まれている割合が95%に近い値になるのか試してみました。
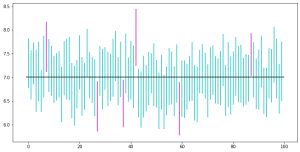
対象とする分布は $N(7, 2^2)$, 一回の標本のサイズは50、実験回数は100としました。
試したコードがこちらです。
from scipy.stats import norm
from scipy.stats import t
import numpy as np
import matplotlib.pyplot as plt
# 母集団の平均と標準偏差を定義
mu = 7
sigma = 2
# サンプルサイズ(一回の実験で撮る標本数)とサンプル数(標本のセットの数)
sample_size = 50
sample_count = 100
# 1-alpha が 0.95 なので、 alpha ha 0.05
alpha = 0.05
# 母集団が従う確率分布
norm_rv = norm.freeze(loc=mu, scale=sigma)
# 区間推定の計算に使う、自由度が sample_size - 1 のt分布
t_rv = t.freeze(sample_size-1)
# 計算した信頼区間たちを格納しておく配列
result = []
for i in range(sample_count):
sample = norm_rv.rvs(size=sample_size)
ave = sample.mean()
s = sample.std()
L = ave - t_rv.isf(alpha/2) * s/np.sqrt(sample_size)
U = ave + t_rv.isf(alpha/2) * s/np.sqrt(sample_size)
result.append([L, U])
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1)
for i, r in enumerate(result):
# 真の平均が信頼区間の中に入っているかどうかで色を変える
if r[0] > mu or r[1] < mu:
color = 'm'
else:
color = 'c'
ax.vlines(x=i, ymin=r[0], ymax=r[1], colors=color)
# 真の平均の値で横線を引く
ax.hlines(y=mu, xmin=-1, xmax=sample_count)
plt.show()
当然ですが途中に乱数を含むので実行のたびに結果が変わります。
外れてしまった(赤っぽく着色されている)のが 6本あり、残り94本が区間内に真の母平均を含む結果になりました。
今回の結果は94%となりましたが、テスト回数が100回だったので十分許容誤差だと思います。
本当に5%くらいは外すんですね。