前回の記事で逆関数法を紹介したので具体的な分布で試そうという趣旨の記事です。
今回は指数分布を使います。(累積分布関数もその逆関数も容易に計算できるから)
まず、指数分布の確率密度関数から。指数分布はパラメータ$\lambda$を一つ持ちます。
$$
f(x) = \left\{
\begin{matrix}
\lambda e^{-\lambda x} & (x \leq 0)\\
0 & (x < 0)
\end{matrix}
\right.
$$
そして、累積分布関数は次のようになります。
$$
F(x) = \left\{
\begin{matrix}
1-e^{-\lambda x} & (x \leq 0)\\
0 & (x < 0)
\end{matrix}
\right.
$$
さらにその逆関数は、こうなります。
$$
F^{-1}(u) = - \frac{1}{\lambda}\log(1-u) \quad (0\leq u <1).
$$
それではPythonで、$[0,1)$の乱数を10000個くらい生成して、
逆関数法で$f(x)$に従う乱数が得られるのか実験してみましょう。
今回は単純のため、$\lambda=1$とします。
Pythonでやってみたコードと結果がこちら。
import numpy as np
import matplotlib.pyplot as plt
# 標準一様分布 に従う乱数を10000個生成する
U_data = np.random.rand(10000)
# 逆関数方法で指数分布に従うデータ生成
result_data = -np.log(1 - U_data)
# ヒストグラムと確率密度関数をプロットする
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
ax.hist(result_data, bins=100, density=True)
ax.plot(np.arange(0, 8, 0.1), np.exp(-1*np.arange(0, 8, 0.1)))
plt.show()
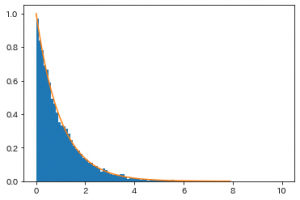
出力。
データ件数が多いので非常に綺麗に出ましたね。