scikit-learnでカーネル密度推定

今回もカーネル密度推定です。前回の記事の予告通り、今回はscikit-learnを使います。

ドキュメントはこちらです: sklearn.neighbors.KernelDensity

scikit-learnの他のモデルと同様に、import してインスタンス作って、fitしたら学習完了、となるのですが、その後の推定に注意することがあります。
version 0.23.1 時点では、他のモデルにある、predict やtransform がありません。
これは代わりに、score_samples を使います。そして戻り値は、
Evaluate the log density model on the data.
とある様に、その点での密度の”対数”です。なので、SciPyの時みたいに密度関数を得たかったら指数関数で変換する必要があります。

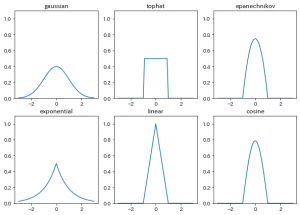
さて、scikit-learn でカーネル密度推定をやるメリットですが、ガウスカーネルだけでなく、全部で6種類のカーネル関数が使えます。

1点だけのデータにたいしてカーネル密度推定を実施すると、そのカーネルの形がそのまま残るのでそれを利用してカーネル関数を可視化しました。


import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity

kernel_names = [
        "gaussian",
        "tophat",
        "epanechnikov",
        "exponential",
        "linear",
        "cosine",
    ]

# x軸のメモリようの配列
xticks = np.linspace(-3, 3, 61)

fig = plt.figure(figsize=(10, 7), facecolor="w")
for i, kernel in enumerate(kernel_names, start=1):
    # 指定したカーネルでモデル作成
    kde_model = KernelDensity(bandwidth=1, kernel=kernel)
    # 1点だけのデータで学習
    kde_model.fit([[0]])
    ax = fig.add_subplot(2, 3, i, title=kernel)
    ax.set_ylim([0, 1.1])
    ax.plot(xticks, np.exp(kde_model.score_samples(xticks.reshape(-1, 1))))

plt.show()

結果がこちら。それぞれ個性ありますね。

さて、カーネル密度推定はscikit-learnで行う場合もバンド幅の決定の問題があります。
そして、SciPyの様に自動的には推定してくれません。

そこで、scikit-learnでは、他のモデルと同じ様に、最適なパラメーターを探索することになります。
Score というメソッドで、与えられたデータに対する対数尤度の合計値が算出できるので、これを使ってグリッドサーチすると良さそうです。
他のどんなモデルもそうなのですが、訓練データと評価データはかならず分ける必要があります。
特にカーネル密度推定では、バンド幅が狭ければ狭いほど訓練データに対するスコアは高くなり、極端に過学習します。
今回は久々にグリッドサーチでもやりましょうか。
また、正解の分布はベータ分布を使います。 (正規分布だとガウスカーネルが有利すぎる気がしたので)

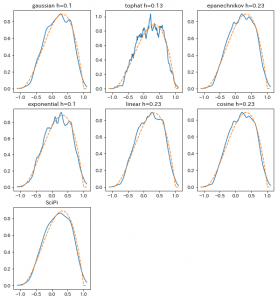
先ほどの６種類のカーネル + SciPyでやってみました。


from scipy.stats import beta
from sklearn.model_selection import GridSearchCV

# グリッドサーチでバンド幅決めてベストのモデルを返す関数
def search_bandwidth(data, kernel="gaussian", cv=5):
    bandwidth = np.linspace(0.1, 2, 190)
    gs_model = GridSearchCV(
                KernelDensity(kernel=kernel),
                {'bandwidth': bandwidth},
                cv=cv
            )
    gs_model.fit(data.reshape(-1, 1))
    return gs_model.best_estimator_

# 正解の分布
frozen = beta(a=3, b=2, loc=-1, scale=2)
# データ生成
data = frozen.rvs(200)

# x軸のメモリようの配列
xticks = np.linspace(-1.1, 1.1, 221)


fig = plt.figure(figsize=(10, 11), facecolor="w")
for i, kernel in enumerate(kernel_names, start=1):
    # 指定したカーネルでモデル作成
    kde_model = search_bandwidth(data, kernel=kernel)
    bw_str = str(kde_model.bandwidth.round(2))
    ax = fig.add_subplot(3, 3, i, title=kernel + " h=" + bw_str)
    # ax.set_ylim([0, 1.1])
    ax.plot(xticks, np.exp(kde_model.score_samples(xticks.reshape(-1, 1))))
    ax.plot(xticks, frozen.pdf(xticks), linestyle="--")

# おまけ。scipy
kde = gaussian_kde(data)
ax = fig.add_subplot(3, 3, 7, title="SciPi")
ax.plot(xticks,  kde.evaluate(xticks))
ax.plot(xticks, frozen.pdf(xticks), linestyle="--")

plt.show()

結果がこちら。一番手軽に使える SciPyが頑張ってますね。
全データを学習に使えるのも大きいかもしれません。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル