scipy.statsで確率分布を自作する

SciPyのstatsモジュールには非常に多くの確率分布が定義されています。
参考: Statistical functions (scipy.stats) — SciPy v1.12.0 Manual

ほとんどの用途はこれらを利用すると事足りるのですが、自分で定義した確率分布を扱うこともあり、scipyのstatsに用意されているような確率分布と同じようにcdfとかのメソッドを使いたいなと思うことがあります。

そのような場合、SciPyではscipy.stats.rv_continuousを継承してpdfメソッドを定義することで確率分布を定義でき、そうすれば(計算量や時間の問題などありますが)cdf等々のメソッドが使えるようになります。

参考: scipy.stats.rv_continuous — SciPy v1.12.0 Manual

実はSciPyの元々用意されている確率分布たちもこのrv_continuousを継承して作られているので、それらのソースコードを読むと使い方の参考になります。既存の確率分布等はpdfだけでなく、cdf、sf、ppf、期待値や分散などの統計量などが明示的に実装されていて計算効率よく使えるようになっています。

しかし先ほども述べた通り、pdf以外は必須ではなく実装されていなければpdfから数値的に計算してくれます。(ただ、予想外のところで計算が終わらなかったり精度が不十分だったりといった問題が起きるので可能な限り実装することをお勧めします。)

確率分布クラスの自作方法

さて、それでは実際にやってみましょう。既存に存在しない例が良いと思うので、正規分布を2個組み合わせた、山が2個ある分布を作ってみます。

クラスを継承して _pdf (pdfではない) メソッドをオーバーライドする形で実装します。

import numpy as np
from scipy.stats import rv_continuous
import matplotlib.pyplot as plt


# 確率密度関数の定義
def my_pdf(x):
    curve1 = np.exp(-(x+3)**2 / 2) / np.sqrt(2 * np.pi)
    curve2 = np.exp(-(x-3)**2 / 2) / np.sqrt(2 * np.pi)

    return (curve1 + curve2)/2


# rv_continuousクラスのサブクラス化
class MyDistribution(rv_continuous):
    def _pdf(self, x):
        return my_pdf(x)


# 分布のインスタンス化
my_dist = MyDistribution(name='my_dist')


# 可視化
x = np.linspace(-6, 6, 121)
fig = plt.figure(facecolor="w", figsize=(8, 8))
ax = fig.add_subplot(2, 2, 1, title="pdf")
ax.plot(x, my_dist.pdf(x))

ax = fig.add_subplot(2, 2, 2, title="cdf")
ax.plot(x, my_dist.cdf(x))

ax = fig.add_subplot(2, 2, 3, title="sf")
ax.plot(x, my_dist.sf(x))

ax = fig.add_subplot(2, 2, 4, title="logpdf")
ax.plot(x, my_dist.logpdf(x))

plt.show()

結果がこちらです。

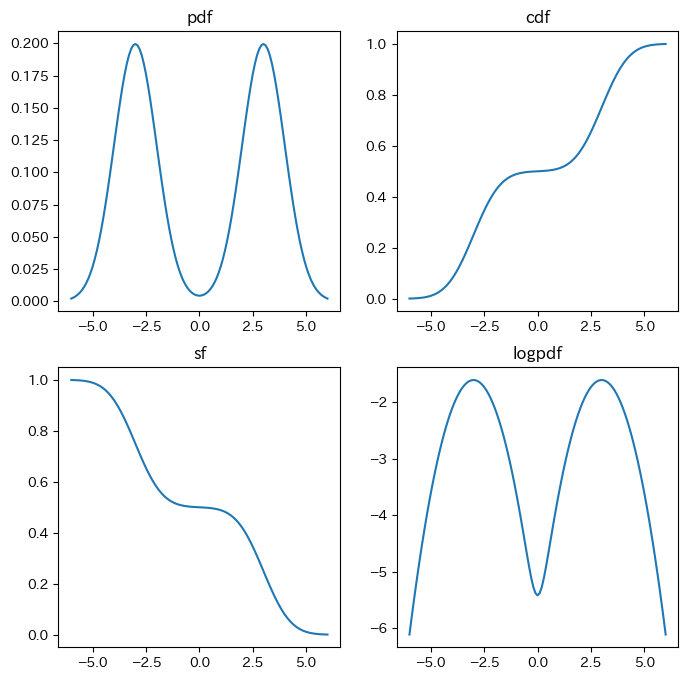
実装したのはpdfだけでしたが、cdfやsf、logpdfなども動いていますね。
繰り返しになりますが、これらは数値計算されたものなので十分注意して扱ってください。特に精度と計算量はもちろんですが、指数関数等もからむので、極端な値を入れたら計算途中でオーバーフローが起きたりもします。重要なものは_pdfと同様に_cdfなどとして明示的に定義した方が良いでしょう。

たとえば、先ほどの分布は分散の計算に少し時間がかかります。

%%time
my_dist.var()
"""
CPU times: user 8.02 s, sys: 146 ms, total: 8.16 s
Wall time: 8.06 s
10.000000000076088
"""

確率密度関数を用意するときの注意点

確率密度関数を自分で作りましたが、この内容に対してのバリデーションなどは用意されていないので自分で責任を持って管理する必要があります。

たとえば、変数xの定義域で正であること、定義域全体で積分したら1になることなどは事前に確認しておく必要があります。(確率密度関数の定義を満たしてないととcdfなど他のメソッドが変な動きをします)

確率分布の台が有限の場合

もう一点、先ほどの2山の分布はxが$-\infty$から$\infty$の値を取る分布でしたが、確率分布の中にはそうではないものもあります。正の範囲でしか定義されない対数正規分布や指数分布、有限区間でしか定義されないベータ分布などですね。

これらについては、「分布のインスタンス化」を行うタイミングで台の下限上限をそれぞれa, b という引数で行います。省略した方は$-\infty$もしくは$\infty$となります。

確率密度関数が上に凸な放物線で定義された分布でやるとこんな感じです。

def my_pdf2(x):
    return 6*x*(1-x)


class MyDistribution2(rv_continuous):
    def _pdf(self, x):
        return my_pdf2(x)


# 分布のインスタンス化
my_dist2 = MyDistribution2(a=0, b=1, name='my_dist2')

以上が、SciPyで連続確率分布インスタンスを自作する方法でした。