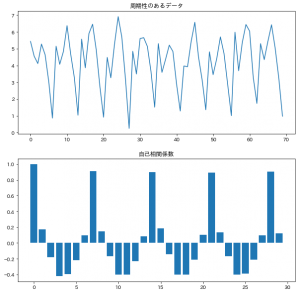
前回の記事で定義した定常過程の例を紹介します。
(今回も沖本本からの引用です。)
iid系列
iid系列は、強定常過程の例です。
定義:
各時点のデータが互いに独立でかつ同一の分布に従う系列はiid系列と呼ばれる。
iidとは、 independent and identically distributedの略です。
Wikipedia : 同時独立分布
$y_t$が期待値$\mu$,分散$\sigma^2$のiid系列であることを $y_t\sim iid(\mu,\sigma^2)$と書きます。
ホワイトノイズ
独立性や同一分布性は非常に強い仮定なのですが、
実用上、モデルの錯乱項などとして使うのであればもう少し弱い仮定で十分です。
そこで次のホワイトノイズというものが使われます。
ホワイトノイズは弱定常過程です。
定義:
すべての時点$t$において
$$
\begin{align}
E(\varepsilon _t) &=0\\
\gamma _k &= E(\varepsilon _t \varepsilon _{t-k}) =\left\{
\begin{array}{ll}
\sigma^2, & (k=0)\\
0, & (k\neq 0)
\end{array}\right.
\end{align}
$$
が成立するとき, $\varepsilon _t$はホワイトノイズ(white noise)と呼ばれる.
$\varepsilon _t$が分散$\sigma^2$のホワイトノイズであることを $\varepsilon _t\sim W.N.(\sigma^2)$と書きます。
次のようにホワイトノイズを使って、基礎的な弱定常過程の例を作れます。
$$
y_t = \mu + \varepsilon _t,\ \ \ \varepsilon _t\sim W.N.(\sigma^2)
$$
自分だけかもしれないのですが、ホワイトノイズと聞くと無意識に$(\varepsilon _t,\cdots,\varepsilon _{t+k})$の同時分布が期待値0の多変量正規分布であるかのようにイメージしてしまいます。
しかし定義の通り、ホワイトノイズにはそこまでの強い仮定はないので注意です。
ちなみに $(y_t,\cdots,y_{t+k})$の同時分布が多変量正規分布の場合、それは正規過程と呼ばれ、
正規過程に従うホワイトノイズは正規ホワイトノイズと呼ばれます。(沖本本のp9,p12)
正規ホワイトノイズはiid過程なので、強定常過程になります。