月: 2023年3月

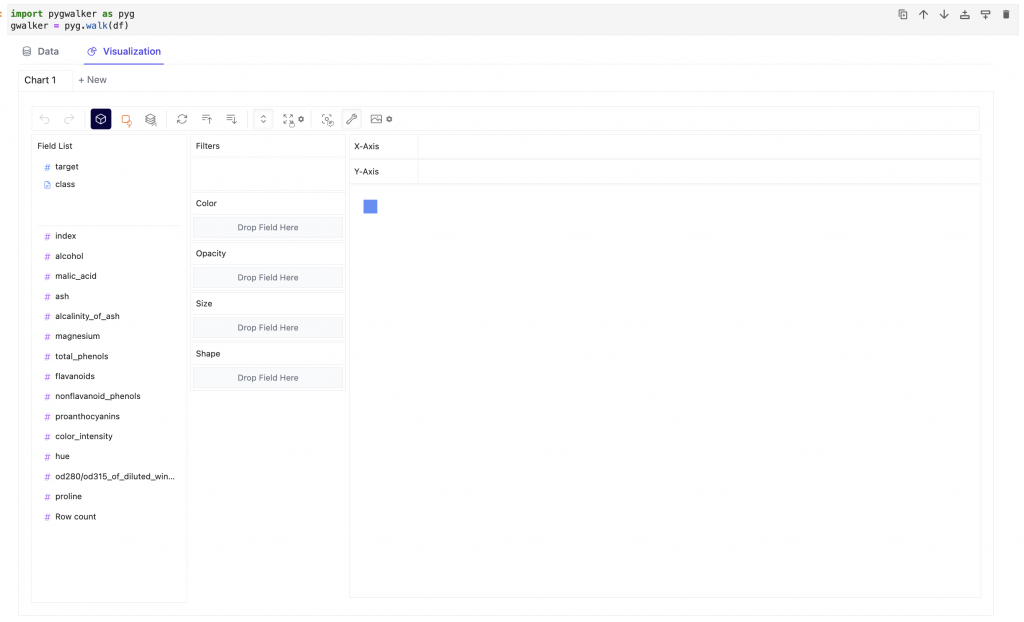
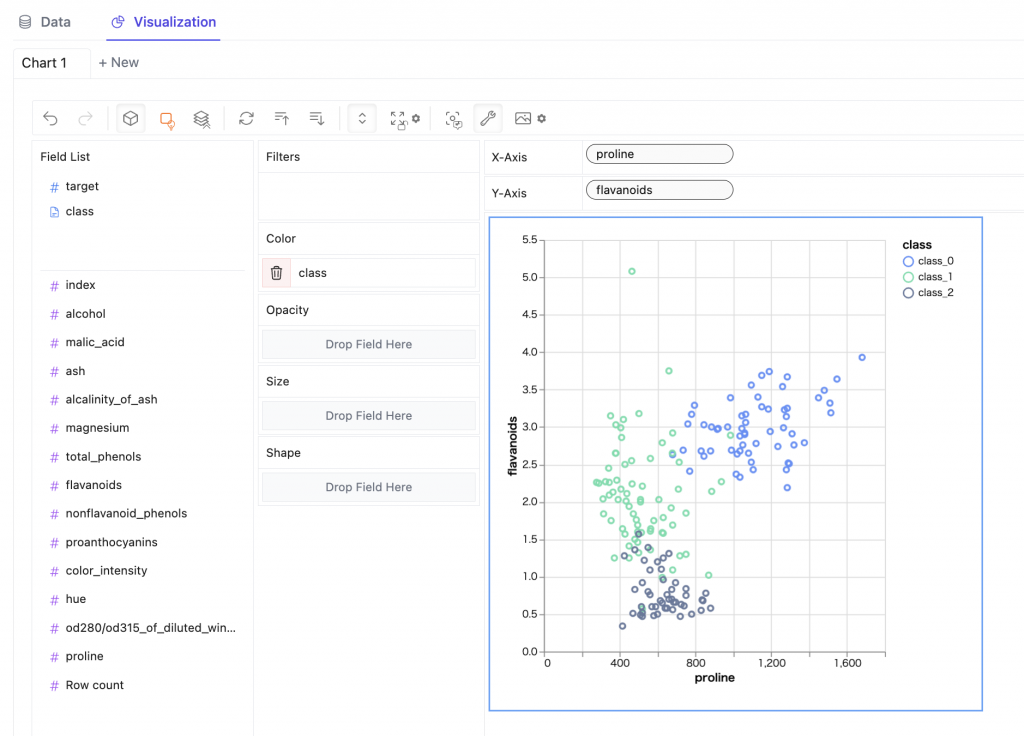
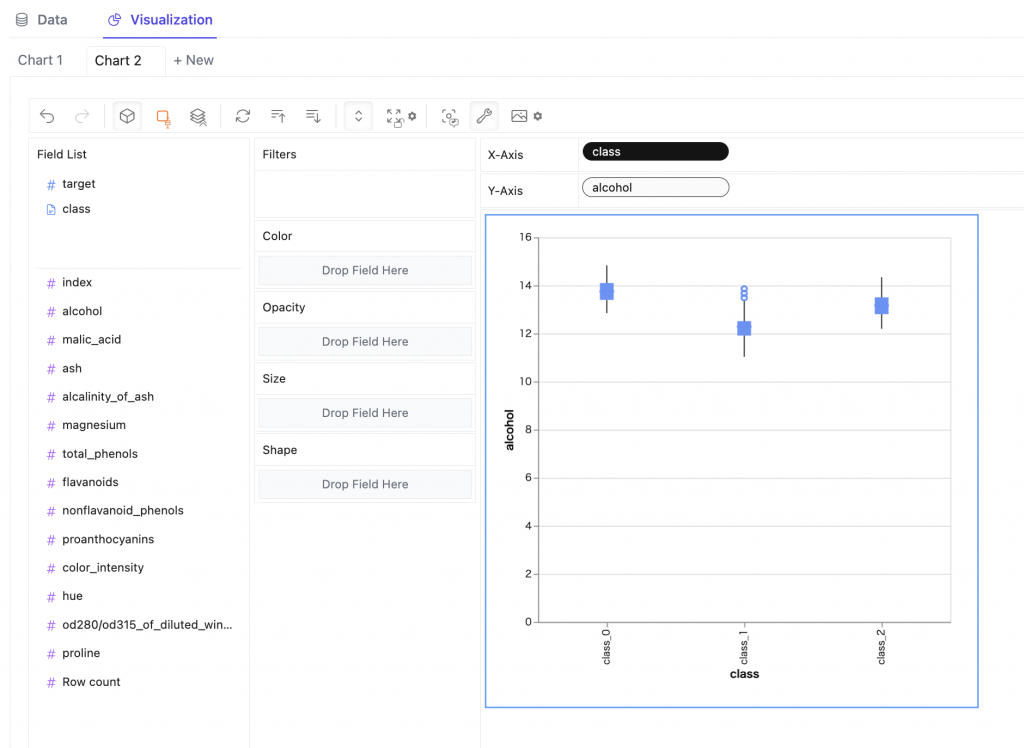
matplotlibでオリジナルの配色を使いたかったのでその方法を調べました。基本的にグラフを書くときにそれぞれのメソッドの引数で逐一RGBの値を指定していっても独自カラーを使うことはできるのですが、カラーマップとして作成すると、既存の配色と同じような雰囲気で使うことができるので便利です。

既存のカラーマップでも利用されている、以下の二つのクラスを使って作成できます。
– matplotlib.colors.ListedColormap (N色の色を用意して選択して使う)
– matplotlib.colors.LinearSegmentedColormap (線形に連続的に変化する色を使う)

上記のリンクがそれぞれのクラスのドキュメントですが、別途カラーマップ作成のページもあります。
– Creating Colormaps in Matplotlib — Matplotlib 3.7.1 documentation

まず、ListedColormapのほうから試してみましょう。これはもう非常に単純で、色のリストを渡してインスタンスを作れば完成です。また、name引数で名前をつけておけます。省略するとname=’from_list’となり、わかりにくいので何かつけましょう。名前をつけておくとregisterってメソッドでカラーマップの一覧に登録することができ、ライブラリの既存のカラーマップと同じように名前で呼び出せるようになります。

それでは適当に、赤、緑、青、黄色、金、銀の6色で作ってみます。色の指定はRGBコードの文字列、0~1の実数値3個のタプル、matplotlibで定義されている色であれば色の名前で定義できます。例として色々試すためにそれぞれやってみます。

from matplotlib.colors import ListedColormap
import matplotlib as mpl
import numpy as np

colors = [
    "#FF0000",  # 赤
    (0, 1, 0),  # 緑
    (0, 0, 1, 1),  # 青(不透明度付き)
    "yellow",
    "gold",
    "silver",
]
pokemon_cmap = ListedColormap(colors, name="pokemon")

# 配色リストに登録するとnameで使えるようになる。(任意)
mpl.colormaps.register(pokemon_cmap)

これで新しいカラーマップができました。試しに使ってみましょう。文字列でつけた名前を渡してもいいし、先ほど作ったカラーマップのインスタンスを渡しても良いです。

# データを作成
np.random.seed(0)
data = np.random.randn(10, 10)

# 作図
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(1, 1, 1)
psm = ax.pcolormesh(data, cmap="pokemon")
# psm = ax.pcolormesh(data, cmap=pokemon_cmap)  # 名前でななくカラーマップインスタンスを渡す場合
fig.colorbar(psm, ax=ax)
plt.show()

このような図ができます。色が適当なので見やすくはありませんが、確かに先ほど指定した色たちが使われていますね。

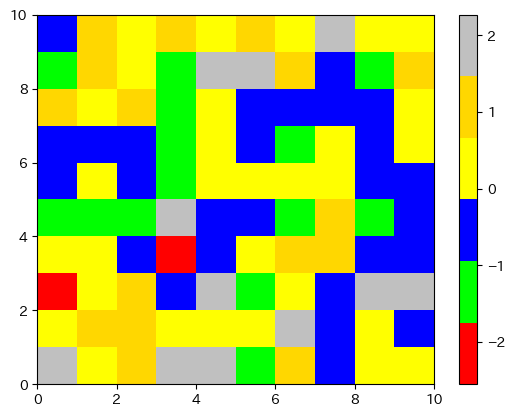
次は連続的に値が変化するLinearSegmentedColormapです。これは色の指定がものすごくややこしいですね。segmentdataっていう、”red”, “green”, “blue”というRGBの3色のキーを持つ辞書データで、それぞのチャネルの値をどのように変化させていくのかを指定することになります。サンプルで作られているデータがこれ。

cdict = {'red':   [(0.0,  0.0, 0.0),
                   (0.5,  1.0, 1.0),
                   (1.0,  1.0, 1.0)],

         'green': [(0.0,  0.0, 0.0),
                   (0.25, 0.0, 0.0),
                   (0.75, 1.0, 1.0),
                   (1.0,  1.0, 1.0)],

         'blue':  [(0.0,  0.0, 0.0),
                   (0.5,  0.0, 0.0),
                   (1.0,  1.0, 1.0)]}

各キーの値ですが3値のタプルのリストになっています。

リスト内のi番目のタプルの値を(x[i], y0[i], y1[i]) とすると、x[i]は0から1までの単調に増加する数列になっている必要があります。上の例で言えば、x[0]=0でx[1]=0.5でx[2]=1なので、0~0.5と0.5~1の範囲のredチャンネルの値の変化がy0,y1で定義されています。

値がx[i]からx[i+1]に変化するに当たって、そのチャンネルの値がy1[i]からy0[i+1]へと変化します。上記の”red”の例で言えば値が0〜0.5に推移するに合わせて0から1(255段階で言えば
255)へと変化し、値が0.5~1と推移する間はずっと1です。

y0[i]とy1[i]に異なる値をセットするとx[i]のところで不連続な変化も起こせるみたいですね。

あと、連続値とは言え実装上はN段階の色になる(そのNが大きく、デフォルトで256段階なので滑らかに変化してるように見える)ので、そのNも指定できます。

とりあえず上のcdictデータでやってみましょう。

newcmp = LinearSegmentedColormap('testCmap', segmentdata=cdict, N=256)

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

pms = ax.pcolormesh(data, cmap=newcmp)
fig.colorbar(pms, ax=ax)
plt.show()

結果がこちら。

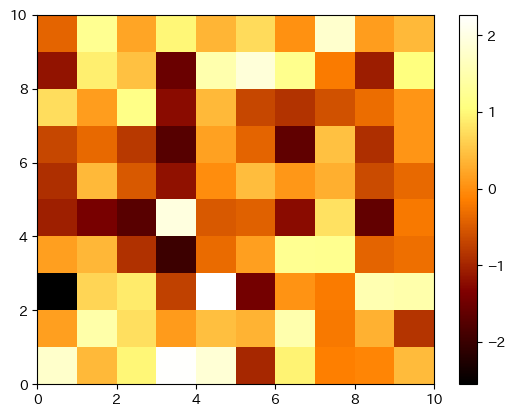
値が小さい時はRGBが全部0なので黒くて、徐々に赤みを増し、途中から緑の値も増え始めるので黄色に向かって、さらに途中から青も増え始めるので最大値付近では白になっていってます。わかりやすいとは言い難いですがなんとなく挙動が理解できてきました。

流石にこのやり方で細かい挙動を作っていくのは大変なので、LinearSegmentedColormap.from_listっていうstaticメソッドがあり、こちらを使うとただ色のリスト渡すだけで等間隔にカラーマップ作ってくれるようです。

また、その時zipを使って区間の調整もできます。使用例の図は省略しますが次のように書きます。(ドキュメントからそのまま引用。)

colors = ["darkorange", "gold", "lawngreen", "lightseagreen"]
cmap1 = LinearSegmentedColormap.from_list("mycmap", colors)

nodes = [0.0, 0.4, 0.8, 1.0]
cmap2 = LinearSegmentedColormap.from_list("mycmap", list(zip(nodes, colors)))

これのほうがずっと楽ですね。

以前、MeCabのユーザー辞書に単語を追加する方法を紹介しました。
参考: MeCabでユーザー辞書を作って単語を追加する
(この記事の本題とずれますが、M1/M2チップのMacではいろんなファイルのパスが変わっているのでこちらの記事を参照される際はご注意ください。)

実際、先ほどの記事を参照してどんどん単語を追加してくと、追加したのに形態素解析結果に反映されないということがあります。というよりも、そもそもデフォルトのIPA辞書でさえ正しい単語が追加されているのにそれが使われずに誤った分割がされることがあります。

このような場合、多くのケースで単語の生起コストを修正することで対応可能です。
シンプルに、MeCabに使って欲しい単語の生起コストを下げるだけです。ただ、あまりに極端に下げてしまうと逆にその低すぎる生起コストのせいで分割すべき場合でも分割されないという事象が発生しえます。

そこで、どの程度生起コストを下げたらいい感じで分割ができるようになるのかというのを探っていこうというのがこの記事です。

例として、今回は「高等学校」って単語でテストしていきましょう。いろんな個別の高等学校の学校名が固有名詞としてIPA辞書に登録されているのに、なぜか一般名詞の「高等学校」が登録されてないのですよね。

ユーザー辞書の登録の記事に沿ってseedファイルを用意し、コストを推定すると、
高等学校,1285,1285,5078,名詞,一般,,,,,高等学校,コウトウガッコウ,コートーガッコー
となり、生起コストは5078となります。

これをコンパイルして、 sample.dic ってユーザー辞書を作っておきます。

さて、適当に例文を作って形態素解析してみましょう。

import pandas as pd
import subprocess
import MeCab


# サンプルデータ生成
sample_texts = [
    "九州高等学校ゴルフ選手権",
    "地元の高等学校に進学した",
    "帝京高等学校のエースとして活躍",
    "開成高等学校117人が現役合格",
    "マンガを高等学校の授業で使う",
]
df = pd.DataFrame({"text": sample_texts})

# MeCabの辞書のパス取得
dicdir = subprocess.run(
    ["mecab-config", "--dicdir"],
    capture_output=True,
    text=True,
).stdout.strip()
sysdic = f"{dicdir}/ipadic"

# 分かち書き用のTagger
tagger_w = MeCab.Tagger(f"-O wakati -d {sysdic} -u sample.dic")

print(df["text"].apply(tagger_w.parse).str.strip())
"""
0          九州 高等 学校 ゴルフ 選手権
1       地元 の 高等 学校 に 進学 し た
2     帝京 高等 学校 の エース として 活躍
3    開成 高等 学校 117 人 が 現役 合格
4     マンガ を 高等 学校 の 授業 で 使う
Name: text, dtype: object
"""

はい、以上の最後の結果の通り、「高校」と「学校」の間にスペースが入っていてせっかく追加した「高等学校」は使われませんでした。ちなみに、Nベスト解を出すと２番目以降に登場するので、ユーザー辞書には正常に追加されています。

print(df["text"].apply(lambda x: tagger_w.parseNBest(2, x)).str.strip())
"""
0                九州 高等 学校 ゴルフ 選手権 \n九州 高等学校 ゴルフ 選手権
1          地元 の 高等 学校 に 進学 し た \n地元 の 高等学校 に 進学 し た
2      帝京 高等 学校 の エース として 活躍 \n帝京 高等学校 の エース として 活躍
3    開成 高等 学校 117 人 が 現役 合格 \n開成 高等学校 117 人 が 現役 合格
4      マンガ を 高等 学校 の 授業 で 使う \nマンガ を 高等学校 の 授業 で 使う
"""

なぜこうなるのか、というと「高等」の生起コストが924、「学校」の生起コストが1624とどちらもとても低いんですよね。両単語間の連接コストが1028ありますが、それを考慮しても、924+1624+1028=3576で、「高等学校」一単語の生起コスト5078よりも低いです。

また、「高等」は名詞,形容動詞語幹なので、前の単語との連接コストも変わってきます。

そのため、追加した「高等学校」を単語として使ってもらうためには、生起コストをモデルが推定した値そのままではなくもっと低く設定してあげる必要があります。

さて、ここからどのくらい生起コストを下げていくらにしたらいいのかを探っていきましょう。方法としては、前後の品詞の単語との組み合わせをありうる全パターン考慮して生起コスト、連接コストから計算することも可能ですが、これは極端に低い値に設定する必要が出ることもあり、逆に分割誤りを誘発することもあるので、もっと具体的に正しく分割されて欲しい例文を基準に計算するのがおすすめです。この記事では先ほど使った5文を使います。

その方法は単純で、「高等」「学校」に割れてしまう分割のコストの総和と、制約付き解析で求める「高等学校」を強制的に使った分割のコストの差分を求めてその分を調整します。

# 生起コスト+連接コストの累積だけを返すTagger
tagger_pc = MeCab.Tagger(f"-F '' -E %pc -d {sysdic} -u sample.dic")
# それの制約付き解析版
tagger_p_pc = MeCab.Tagger(f"-p -F '' -E %pc -d {sysdic} -u sample.dic")

target_word = "高等学校"

# コストの合計をそれぞれ求める
df["コスト合計"] = df["text"].apply(lambda x: tagger_pc.parse(x)).astype(int)
# 制約付きの方は、制約をつけたい単語は 単語\t* 形式に置き換えて実行
df["制約付き解析コスト合計"] = df["text"].apply(
    lambda x: tagger_p_pc.parse(x.replace(target_word, f"\n{target_word}\t*\n"))
).astype(int)
# コストの差分を計算
df["コスト差分"] = df["制約付き解析コスト合計"] - df["コスト合計"]

# 結果表示
print(df)
"""
              text  コスト合計  制約付き解析コスト合計  コスト差分
0     九州高等学校ゴルフ選手権   6901         7495    594
1     地元の高等学校に進学した  10811        11807    996
2  帝京高等学校のエースとして活躍  15034        15484    450
3  開成高等学校117人が現役合格  40123        40138     15
4   マンガを高等学校の授業で使う  10407        12945   2538
"""

最後の例だけコスト差分がとにかく多いのは、を(助詞,格助詞,一般)と高等(名詞,形容動詞語幹)の連接コストが-1550と非常に小さいのも影響しています。

さて、これらの5文章で分割を正確にしたかったら、「高等学校」生起コストを2539下げれば大丈夫そうです。ただ、その前にちょっと実験として、996だけ小さくして、$5078-996=4082$に設定してみましょう。0,2,3番目はこれで正常に修正されるはず、4番目の文は修正されないはず、1番目はどうなるかみてみたいですね。

高等学校,1285,1285,4082,名詞,一般,,,,,高等学校,コウトウガッコウ,コートーガッコー

でユーザー辞書 sample2.dic を作ってみました。実験結果がこちら。

# 分かち書き用のTagger
tagger_w_2 = MeCab.Tagger(f"-O wakati -d {sysdic} -u sample2.dic")

print(df["text"].apply(tagger_w_2.parse).str.strip())
"""
0          九州 高等学校 ゴルフ 選手権
1      地元 の 高等 学校 に 進学 し た
2     帝京 高等学校 の エース として 活躍
3    開成 高等学校 117 人 が 現役 合格
4    マンガ を 高等 学校 の 授業 で 使う
Name: text, dtype: object
"""

ほぼ想定通りで、1番目のやつはシステム辞書の単語たちがそのまま使われましたね。もう1だけ下げる必要があったようです。

結果は省略しますが、もう一つだけコストを下げて4081にすると、1番目の文も正しく「高等学校」が単語として扱われます。

$5078-2538-1=2539$まで下げれば5文とも正しくなりますね。元のコストから見るとかなり低くしたように見えますが、「学校」の生起コストが1624なでのまぁ許容範囲でしょう。

以上の処理をメソッド化して、適切なコストを返してくれる関数を作るとしたらこんな感じでしょうか。あまり綺麗なコードじゃないのでもう少し考えたいですね。

wordで渡す引数はすでにユーザー辞書に登録済みで品詞等は判明していてあとはコスト調整だけの問題になっていることや、sentenceの中では正確に1回だけ登場することなど制約が多いのでかなり利用に注意が必要です。頻繁に必要になるようならまた改めて考えようと思います。

dicdir = subprocess.run(
    ["mecab-config", "--dicdir"],
    capture_output=True,
    text=True,
).stdout.strip()
sysdic = f"{dicdir}/ipadic"
# 単語の生起コストを出すTagger
tagger_p_c = MeCab.Tagger(f"-p -F %c -E '' -d {sysdic} -u sample.dic")
# コストの総和を出すTagger
tagger_pc = MeCab.Tagger(f"-F '' -E %pc -d {sysdic} -u sample.dic")
# 制約付き解析でコストの総和を出すTagger
tagger_p_pc = MeCab.Tagger(f"-p -F '' -E %pc -d {sysdic} -u sample.dic")


def calc_adjust_cost(word, sentence):
    all_cost = int(tagger_pc.parse(sentence))
    all_p_cost = int(tagger_p_pc.parse(sentence.replace(word, f"\n{word}\t*\n")))
    current_cost = int(tagger_p_c.parse(f"\n{word}\t*\n"))
    return current_cost - all_p_cost + all_cost - 1


calc_adjust_cost("高等学校", "マンガを高等学校の授業で使う")
# 2539

結果自体は正しそうですね。

最近、TwitterでPyGWalkerというライブラリを知りました。
Githubで最初のコミットを見ると、2023/2/16の登場でまだ1ヶ月もたってない新しいライブラリです。

これが何かというと、JupyterでTableau風にDataFrameを可視化するライブラリになります。
(あくまでもTableau風であって互換というわけではないですが。)
Tableau好きな自分にとってはキャプチャ画像で見た第一印象が衝撃的だったので早速使ってみることにしました。

PyPiのページはこちらです。
参考: pygwalker · PyPI

インストールは普通にpipでできます。この記事を書いてる時点で入ったバージョンは pygwalker==0.1.4.9.post0 でした。

$ pip install pygwalker

早速これ使ってみましょう。使い方は簡単で、import して、walkメソッドに可視化したいデータフレームを渡すだけです。
とりあえず、scikit-learnのサンプルデータでやってみましょうかね。特に理由はないですが特徴量が比較的多様なwineを使います。まずデータフレーム作成から。

import pandas as pd
from sklearn.datasets import load_wine


# データ読み込み
wine = load_wine()
# 特徴量名を列名としてDataFrame作成
df = pd.DataFrame(
    wine.data,
    columns=wine.feature_names,
)

# target列も作成する。
df["target"] = wine.target
df["class"] = df["target"].apply(lambda x: wine["target_names"][x])

そして、次のコードでPyGWalkerが起動できます。Githubのサンプルに沿ってpygの名前でインポートしました。

import pygwalker as pyg


gwalker = pyg.walk(df)

そうすると以下のUIが表示されます。だいぶTableauそっくりじゃないですか？

とりあえず特徴量を2個選んで散布図でも作ってみましょう。prolineを X-Axis, flavanoidsをY-Axisのところにドラッグします。また、classで色分けしたいので、ColorのところにClassを持っていきます。この時点で、classごとに集計された3点の散布図になってるので、上の画像で黒反転してる立方体をクリックして集計を解除し個別プロットに変形します。グラフが少し小さいので、Layoutの設定もいじって拡大します。結果できるのが次のグラフです。

非集約化の捜査がちょっと独特でしたが、だいぶTableauライクな操作でいい感じの図が作れたと思います。

色を好みのものに変えたりとか、軸の細かい設定とかそういうTableauでならできる機能が色々なかったりしますが、それは今後のバージョンアップに期待しましょう。

オレンジのアイコンでグラフの種類も変えられます。折れ線グラフ、棒グラフ、円グラフなどの定番に加えて、Boxプロットとかもあるのもいいですね。
たとえば、Boxプロットを使うと次のようなグラフが作れます。

今のままの使い勝手だったら、to_csv して本家Tableauで表示するか、matplotlib使うかする方が便利かなぁとも思うのですが、なんせ登場してまだ1ヶ月未満で、バージョン0.1台のライブラリであり、頻繁に更新が入っている状況です。
これからの発展に期待したいですね。

最近書いたSVARモデルの話や、以前書いたVARモデルの直交化インパルス応答の話と少し関係あるのですが、コレスキー分解と言う行列分解があります。これをNumpyで行う方法を紹介しておこうと言う記事です。

参考: コレスキー分解 – Wikipedia

Wikipediaでは正定値エルミート行列について定義が書いてありますが一旦、実行列をメインで考えるのでその直後に書いてある実対称行列の話で進めます。
正定値実対称行列$\mathbf{A}$を下三角行列$\mathbf{L}$とその転置行列$\mathbf{L}^T$の積に分解するのがコレスキー分解です。

NumpyやScipyには専用のメソッドが実装されおり、容易に行うことができます。NumpyでできるならNumpyでやってしまうのがオススメです。(scipyの方はなぜか上三角行列がデフォルトですし。)
参考: numpy.linalg.cholesky — NumPy v1.24 Manual
scipy.linalg.cholesky — SciPy v1.10.1 Manual

では適当な行列用意してやってみましょう。

import numpy as np


# 適当に正定値対称行列を用意する
A = np.array([
    [2, 1, 3],
    [1, 4, 2],
    [3, 2, 6],
])

# 一応正定値なのを見ておく
print(np.linalg.eigvals(A))
# array([8.67447336, 0.39312789, 2.93239875])

# コレスキー分解とその結果を表示
L = np.linalg.cholesky(A)
print(L)
"""
[[1.41421356 0.         0.        ]
 [0.70710678 1.87082869 0.        ]
 [2.12132034 0.26726124 1.19522861]]
"""

# 転置行列と掛け合わせることで元の行列になることを確認
print(L@L.T)
"""
[[2. 1. 3.]
 [1. 4. 2.]
 [3. 2. 6.]]
"""

簡単でしたね。

さて、ここまでだとメソッド一つ紹介しただけなのですが、実はここからが今回の記事の本題です。Wikipediaには修正コレスキー分解ってのが紹介されています。これは元の行列を対角成分が全て1の下三角行列$\mathbf{P}$と、対角行列$\mathbf{D}$と、1個目の三角行列の転置行列$\mathbf{P^T}$の3つの積に分解する方法です。(Wikipedia中の式ではこの三角行列もLになってますが、先出のLと被ると以降の説明が書きにくいのでここではPとします。)
$$\mathbf{A}=\mathbf{PDP^T}$$
と分解します。

直交化インパルス応答関数の記事中で使ってるのはこちらなのですが、どうやらこれをやってくれる関数が用意されてないのでやってみました。
いやいや、このメソッドがあるじゃないか、と言うのをご存知の人がいらっしゃいましたら教えてください。

さて、僕がやった方法ですがこれは単純で、コレスキー分解の結果をさらに分解し、
$$\mathbf{L}=\mathbf{PD^{1/2}}$$
とすることを目指します。

ちょっと計算するとすぐわかるのですが、下三角行列$\mathbf{L}$を対角成分が1の下三角行列と対角行列の積に分解しようとしたら、対角行列の方は元の三角行列の対角成分を取り出したものにするしかありません。あとはそれ使って$\mathbf{P}$も計算したら完成です。

対角成分を取り出した行列はnumpy.diagを使います。これ2次元配列に使うと対角成分を1次元配列で取り出し、1次元配列を渡すとそこから対角行列を生成すると言うなかなかトリッキーな動きをするので、対角成分を取り出して対角行列を作りたかったらこれを2回作用させます。平方根も外すために2乗することも忘れないようにすると、$\mathbf{D}$は次のようにして求まり、さらにその逆行列を使って$\mathbf{P}$も出せます。

# 対角行列Dの計算
D = np.diag(np.diag(L))**2
print(D)
"""
[[2.         0.         0.        ]
 [0.         3.5        0.        ]
 [0.         0.         1.42857143]]
"""

# Dを用いて、対角成分1の下三角行列Pを求める
P = L@np.linalg.inv(D**0.5)
print(P)
"""
[[1.         0.         0.        ]
 [0.5        1.         0.        ]
 [1.5        0.14285714 1.        ]]
"""

# PDP^tで元の行列Aが復元できることを見る
print(P@D@P.T)
"""
[[2. 1. 3.]
 [1. 4. 2.]
 [3. 2. 6.]]
"""

はい、これでできました。ブログの都合上、逐一printして出力も表示してるのでめんどくさそうな感じになってますが、実質以下の3行で実装できています。

L = np.linalg.cholesky(A)
D = np.diag(np.diag(L))**2
P = L@np.linalg.inv(D**0.5)