データの傾向を見るときにヒストグラムを描くことは頻繁にありますが、
そのとき課題になるのが、ビンの数を何本にするかです。
いつもmatplotlibのデフォルトである10本でとりあえず試したり、
適当に変えながら何パターンか試したりしています。
Tableauであれば、本数ではなく幅での指定ですね。
ただ、何かしら参考指標が欲しいとは思っていたので調べたところ、複数の方法が提案されていました、
その中でスタージェスの公式(Sturges’ formula)が良さそうだったので試してみました。
定義はwikipediaのものを採用しましょう。
(他のサイトを見ると、小数点以下の扱いで微妙に異なるパターンがあります。)
ヒストグラム – Wikipedia
スタージェスの公式によると、n個のデータがあるとき、ビンの数kの目安は次の式で得られます。
$$k = \lceil \log_{2}{n} + 1\rceil$$
注意として、スタージェスの公式はその導出の背景に、二項分布が正規分布で近似できるという性質を使っています。
そのため、nが小さすぎる場合にはあまり参考になりません。
(そのような時はそもそも、ヒストグラム自体があまり有効ではないです。)
また、 データの分布が二項分布/正規分布と大きく異なる時もうまくいきません。
それではいくつかのデータで試してみましょう。
次のコードは、7種類の件数に対して、ランダムにデータを取得し、
スタージェスの公式で得られたビンの数ののヒストグラム(中央列)と、
それよりビンが2本少ないヒストグラム(左列)、2本多いヒストグラム(右列)を描写します。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def sturges_formula(data_size):
return int(np.floor(1+np.log2(data_size)))
fig = plt.figure(figsize=(15, 28), facecolor="white")
for i in range(7):
data_size = int(1.5 * 2 ** (i+4))
data = np.random.randn(data_size)
bin_count = sturges_formula(data_size)
for j in range(3):
ax = fig.add_subplot(7, 3, 3*i+j+1)
ax.set_title("データ件数:{d}件, ビン:{b}本".format(
d=data_size, b=bin_count-2+2*j
))
ax.hist(data, bins=bin_count-2+2*j, rwidth=0.8)
plt.show()
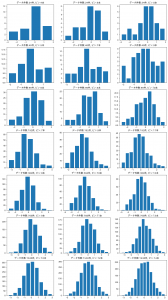
乱数を使っているので毎回結果は変わりますが、出力の一例がこちら。
左列は確かに若干少ないかなという気がします。
ただ、データ件数が多くなると、もう少し多い数(右列)でもいいので、やはり目安として使うのが良さそうですね。