カテゴリー: プログラミング

前回前々回とhyperoptを扱ってきましたが、例があまりにもシンプルだったのでもう少しまともなサンプルを出します。
今回はあらかじめ定義された多変数関数が最大値をとる点を探します。
たった２変数の関数ですが、これ以上変数を増やしても本質的にはやることは変わりません。

きちんと最適解の近くを探していることがわかるように最後に可視化も行います。

例にする関数はこちらです。
$$2*e^{-(x-1)^2-(y-2)^2}+e^{-(x+3)^2-(y+4)^2}$$
点$(1, 2)$からちょっとずれたところで最大値を取りそうな関数ですね。
そして、 点$(-3, -4)$付近にもう一つ山があります。

早速やってみましょう。

import numpy as np
from hyperopt import hp,  fmin, tpe, Trials


# 最大値を探したい関数
def f(x, y):
    return 2 * np.exp(-(x-1)**2 - (y-2)**2) + np.exp(-(x+3)**2 - (y+4)**2)


# 探索する関数を定義する
def objective(args):
    x = args["x"]
    y = args["y"]

    # 最大値を検索するため、マイナスをつけて符号を反転
    return - f(x, y)


# 探索する空間を定義する
space = {
        'x': hp.uniform('x', -5, 5),
        'y': hp.uniform('y', -5, 5)
    }

trials = Trials()

best = fmin(
            fn=objective,
            space=space,
            algo=tpe.suggest,
            max_evals=100,
            trials=trials,
        )

print(best)

# 以下出力
100%|██████████| 100/100 [00:00<00:00, 293.11it/s, best loss: -1.9782848207515258]
{'x': 1.0647780122167085, 'y': 1.9180196819617374}

きちんとそれっぽい点を見つけてきましたね。
これまでの例と違うのは、最小値を探索する関数と、探索する空間が、fminの外側で事前に定義されている点です。

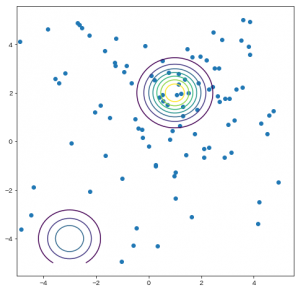
あとは trials オブジェクトの中身を確認し、正解付近を重点的に探索していることを確認しましょう。

import matplotlib.pyplot as plt
X = np.linspace(-5, 5, 100)
Y = np.linspace(-5, 5, 100)
xx, yy = np.meshgrid(X, Y)

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1)
ax.contour(xx, yy, f(xx, yy))
ax.scatter(trials.vals["x"], trials.vals["y"])
plt.show()

できた図がこちらです。

$(-3,-4)$付近はそこそこに、$(1, 2)$付近を重点的に探していることがわかります。

前回の記事に続いて、hyperoptの記事です。
前回のサンプルコードでは、100回の探索を経て見つけた最良の値を取得しましたが、
そのほかの結果もみたいということはあると思います。
機械学習のモデルであれば、どのパラメーターが精度に寄与していたとか、
どれはあまり重要でないとか確認したいですからね。

そのような時、hyperopt では Trials というオブジェクトを使います。
ドキュメントのこちらを参考にやってみましょう。
1.3 The Trials Object

from hyperopt import fmin, tpe, hp, Trials
trials = Trials()
best = fmin(
            fn=lambda x: x ** 2,
            space=hp.uniform('x', -10, 10),
            algo=tpe.suggest,
            max_evals=100,
            trials=trials,
        )
print(best)

# 出力
100%|██████████| 100/100 [00:00<00:00, 554.94it/s, best loss: 8.318492974446729e-09]
{'x': 9.120577270352315e-05}

Trials() ってのが途中で出てきた以外は前回の記事と同じコードですね。
この時、trials変数に100回分の履歴が残っています。
試しに一つ見てみましょう。

# trials.trialsに配列型で格納されている結果の一つ目
trials.trials[0]

# 内容
{'state': 2,
 'tid': 0,
 'spec': None,
 'result': {'loss': 96.69903496469523, 'status': 'ok'},
 'misc': {'tid': 0,
  'cmd': ('domain_attachment', 'FMinIter_Domain'),
  'workdir': None,
  'idxs': {'x': [0]},
  'vals': {'x': [-9.833566746847007]}},
 'exp_key': None,
 'owner': None,
 'version': 0,
 'book_time': datetime.datetime(2019, 3, 10, 15, 4, 45, 779000),
 'refresh_time': datetime.datetime(2019, 3, 10, 15, 4, 45, 779000)}

$x=-9.833566746847007$ を試したら 損失関数$x^2$の値は$96.69903496469523$ だったということがわかります。

このほか、次のような変数にそれぞれの値の辞書も格納されています。
trials.results
trials.vals

せっかくなので、本当に正解の$x=0$付近を探索していたのか可視化してみましょう。

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1)
ax.scatter(trials.vals["x"], trials.losses())
plt.show()

結果がこちら。

きちんと正解付近に点が密集していますね。

昨年参加したpycon2018の
実践・競馬データサイエンス というセッションで知った、hyperopt というライブラリのメモです。
とりあえずこの記事では最もシンプルな例で動かすところまで行きます。
ちなみに、pyconの時の資料はこちら。
実践・競馬データサイエンス

なんでも、ハイパーパラメーターをグリッドサーチなどより効率的に探索してくれるとのこと。

公式サイトの通り、 pipでインストールできます。

pip install hyperopt

早速動かしてみましょう。
Basic tutorial

$x^2$ が最小になる$x$(正解は$x=0$です)を探索するコードです。

from hyperopt import fmin, tpe, hp
best = fmin(
            fn=lambda x: x ** 2,
            space=hp.uniform('x', -10, 10),
            algo=tpe.suggest,
            max_evals=100
        )
print(best)

# 以下出力
100%|██████████| 100/100 [00:00<00:00, 570.89it/s, best loss: 0.0009715421527694116]
{'x': 0.031169570942979175}

これで、 $-10<=x<=10$ の範囲を100回探索し、$x=0.031$あたりで最小と見つけてきたようです。 単純すぎていまいちありがたみが感じられませんね。 ただグリッドサーチと比較すると、仮に-10から10を単純に100分割したら区間の幅は0.2になるわけで、 それよりはずっと小さい誤差で最小値付近の値を見つけています。 (とはいえ、グリッドサーチなら $x=0$をピタリと見つけるとは思いますが。) 機械学習のハイパーパラメーターの探索等で役に立つと聞いて調べたものであり、 僕もそのように使うことが多いので、今後の記事でもう少し細かく紹介しようと思います。 一点気になるのは公式ドキュメントのこの記述。

Hyperopt has been designed to accommodate Bayesian optimization algorithms based on Gaussian processes and regression trees, but these are not currently implemented.

[翻訳]
Hyperoptは、ガウス過程と回帰木に基づくベイズ最適化アルゴリズムに対応するように設計されていますが、これらは現在実装されていません。

Qiitaなどで、hpyeroptをベイズ最適化のライブラリだって紹介している人を見かけたこともあるのですが、そうではなさそうです。