カテゴリー: 時系列分析

今回は2変量のVARモデルにしたがうデータから、Pythonを使ってモデルの係数を推定する方法を紹介します。
答え合わせをしたいので、使うデータは特定のVARモデルから生成します。

モデルはいつもの沖本先生の本のP102ページの演習問題から拝借しました。

$$
\left\{\begin{matrix}\
y_{1t} &=& 2+ 0.5 y_{1,t-1}+ 0.4 y_{2,t-1}+\varepsilon_{1t},\\\
y_{2t} &=& -3 + 0.6 y_{1,t-1}+ 0.3 y_{2,t-1}+\varepsilon_{2t}\
\end{matrix}\
\right.\
\left(\begin{matrix}\varepsilon_{1t}\\\varepsilon_{2t}\end{matrix}\right)\sim W.N.(\mathbf{\Sigma})
$$
$$
\Sigma = \left(\begin{matrix}4&1.2\\1.2&1\end{matrix}\right)
$$

まずはデータを生成します。

import numpy as np
import matplotlib.pyplot as plt

mean = np.array([0, 0])
cov = np.array([[4, 1.2], [1.2, 1]])

# 少し長めの系列でデータを生成する。
data = np.zeros([110, 2])
epsilons = np.random.multivariate_normal(mean, cov, size=110)
print(np.cov(epsilons, rowvar=False))
"""
[[3.96508657 1.1917421 ]
 [1.1917421  1.01758275]]
"""

for i in range(1, 110):
    data[i, 0] = 2 + 0.5*data[i-1, 0] + 0.4*data[i-1, 1] + epsilons[i, 0]
    data[i, 1] = -3 + 0.6*data[i-1, 0] + 0.3*data[i-1, 1] + epsilons[i, 1]

# 初めの10項を切り捨てる
data = data[10:]
# data.shape == (100, 2)

fig = plt.figure(figsize=(12, 5), facecolor="w")
ax = fig.add_subplot(111)
ax.plot(data[:, 0], label="$y_1$")
ax.plot(data[:, 1], label="$y_2$")
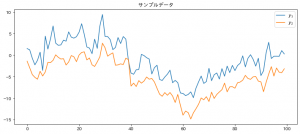
ax.set_title("サンプルデータ")
plt.legend()
plt.show()

生成されたデータをプロットしたのがこちら。

さて、いよいよ statsmodelsでVARモデルのパラメーター推定をやりますが、
方法は非常に簡単で、時系列モデルのapiからVARモデルを呼び出してデータを渡し、学習するだけです。

ドキュメント:
Vector Autoregressions tsa.vector_ar

from statsmodels.tsa.api import VAR
model = VAR(data)
result = model.fit(maxlags=1)
print(result.summary())
"""
  Summary of Regression Results
==================================
Model:                         VAR
Method:                        OLS
Date:           Mon, 03, Feb, 2020
Time:                     01:10:12
--------------------------------------------------------------------
No. of Equations:         2.00000    BIC:                    1.23044
Nobs:                     99.0000    HQIC:                   1.13680
Log likelihood:          -328.071    FPE:                    2.92472
AIC:                      1.07316    Det(Omega_mle):         2.75521
--------------------------------------------------------------------
Results for equation y1
========================================================================
           coefficient       std. error           t-stat            prob
------------------------------------------------------------------------
const         1.879511         0.616917            3.047           0.002
L1.y1         0.464346         0.124135            3.741           0.000
L1.y2         0.462511         0.132200            3.499           0.000
========================================================================

Results for equation y2
========================================================================
           coefficient       std. error           t-stat            prob
------------------------------------------------------------------------
const        -2.683660         0.305923           -8.772           0.000
L1.y1         0.561468         0.061557            9.121           0.000
L1.y2         0.385671         0.065556            5.883           0.000
========================================================================

Correlation matrix of residuals
            y1        y2
y1    1.000000  0.583971
y2    0.583971  1.000000
"""

今回はモデルの形が事前にわかっているので、 maxlags=1 としましたが、 ここを少し大きめの値にしておけば自動的にlagの値を選んでくれます。
選び方は 引数”ic”で指定できます。 (未指定ならAIC)

ic : {‘aic’, ‘fpe’, ‘hqic’, ‘bic’, None}
Information criterion to use for VAR order selection.
aic : Akaike
fpe : Final prediction error
hqic : Hannan-Quinn
bic : Bayesian a.k.a. Schwarz

さて、結果の係数ですが、summaryを見ると大体次の値になっています。(四捨五入しました)
$$
\left\{\begin{matrix}\
y_{1t} &=& 1.89+ 0.46 y_{1,t-1}+ 0.46 y_{2,t-1}\\\
y_{2t} &=& -2.68 + 0.56 y_{1,t-1}+ 0.39 y_{2,t-1}\
\end{matrix}\
\right.\
$$
とても正確というわけではありませんが、概ね正しく推定できていそうです。

前回の記事で弱定常過程の定義をベクトルに拡張しましたが、今回はホワイトノイズをベクトルに拡張した
ベクトルホワイトノイズを定義します。
参考: 定常過程の例としてのiid過程とホワイトノイズ

ベクトル過程 $\boldsymbol{\varepsilon}_t$ が全ての時点 $t$ において次の二つの式を満たすとします。
$$
\begin{align}
E(\boldsymbol{\varepsilon}_t) &= \mathbf{0}&\\
E(\boldsymbol{\varepsilon}_t \boldsymbol{\varepsilon}_{t-k}^{\top}) &=
\left\{
\begin{matrix}
\boldsymbol{\Sigma},& k=0\\\
\mathbf{0},& k\neq 0 \
\end{matrix}
\right.
\end{align}
$$

この時、 $\boldsymbol{\varepsilon}_t$ をベクトルホワイトノイズと呼びます。
このベクトルホワイトノイズは弱定常であり、自己相関を持たないことはすぐわかります。
$k\neq 0$の時、$k$次の自己共分散行列が$\mathbf{0}$ですから。

沖本先生の本で注意されている通り、同時点での各変数は相関を持つことができます。

ただ、一点、次の記載があるのには少し引っかかります。(初版第13刷 P.76)

$\boldsymbol{\Sigma}$ は$n\times n$正定値行列であり、対角行列である必要はないことには注意が必要である.

$n\times n$正定値行列であることは確かなのでしが、これ、必ず対角行列になるような気がします。
というのも、$\boldsymbol{\Gamma}_k = \boldsymbol{\Gamma}^{\top}_{-k}$に、$k=0$ を代入したら、
$\boldsymbol{\Gamma}_0 = \boldsymbol{\Gamma}^{\top}_{0}$ となり、これは対角行列ですよね。

僕が何か勘違いしているのかもしれませんがおそらく誤植か何かのように思います。
(出版社サイトの今日時点の正誤表には入ってないようです)

ベクトル自己回帰モデルについて理解していくにあたって、弱定常過程やホワイトノイズの概念をベクトルに拡張したものを考える必要があるので、
ここで各用語の定義を整理しておきます。(前回の記事と順番前後してしまいました。)
出典は今回も沖本先生の本です。

また、１変数の場合については次の記事をご参照ください。
参考: 確率過程の弱定常性と強定常性

まず、 $\mathbf{y}_t = (y_{1t}, y_{2t}, \ldots, y_{nt})^{\top}$ は $n\times1$の行列(列ベクトル)としておきます。
そして、これの期待値ベクトルは普通に要素ごとの期待値をとって、次のように定義されます。
$$
E(\mathbf{y}_t) = (E(y_{1t}), \ldots, E(y_{nt}))^{\top}.
$$

次に、自己共分散を拡張します。ここからがポイントで、$y_{it}$に対して$y_{i,t-k}$との共分散を考えるだけではなく、
$\mathbf{y}_t$の他の要素の過去の値$y_{j,t-k}$との共分散も考慮します。そのため、結果は次のように行列になります。

そのため、$k$次自己共分散行列は次の$n\times n$行列で定義されます。

$$
\begin{align}
Cov(\mathbf{y}_t, \mathbf{y}_{t-k}) &= [Cov(y_{it},y_{j,t-k})]_{ij}\\
&=\left(\
\begin{matrix}\
Cov(y_{1t},y_{1,t-k}) & \cdots & Cov(y_{1t},y_{n,t-k}) \\\
\vdots & \ddots & \vdots \\\
Cov(y_{nt},y_{1,t-k}) & \cdots & Cov(y_{nt},y_{n,t-k}) \
\end{matrix}\
\right)
\end{align}.
$$

この行列の対角成分は、各変数の$k$次自己共分散に等しくなります。
また、$k=0$の時、$k$次自己共分散行列は、分散共分散行列に等しくなり、対称行列になりますが、
$k\neq 0$の時は、一般には対称行列にならないので注意が必要です。

期待値も$k$次自己共分散行列も定義式の中に$t$が入っているので、
これらは$t$の関数なのですが、この値がどちらも$t$に依存しなかった時、
1変数の場合と同じように、ベクトル過程は弱定常と言われます。

弱定常性を仮定する時は、期待値を$\boldsymbol{\mu}$、$k$次自己共分散行列を$\boldsymbol{\Gamma}_k$と書きます。
なお、$\boldsymbol{\Gamma}_k = \boldsymbol{\Gamma}^{\top}_{-k}$が成り立ちます。(転地を等号が成り立たない点に注意が必要です。)

さて、自己共分散行列は、異なる時点での各変数の関係を表したものですが、各要素の値の大小は単位に依存してしまい、
これだけ見ても関係が強いのか弱いのかわかりません。
そこで、自己共分散行列を標準化した自己相関行列を考えます。
それは次の式で定義されます。
$$
\boldsymbol{\rho}_k = Corr(\mathbf{y}_t, \mathbf{y}_{t-k}) = [Corr(y_{it},y_{j,t-k})]_{ij}.
$$

また、$\mathbf{D} = diag(Var(y_1), \ldots, Var(y_n))$、($\mathbf{y}_t$の分散を対角成分に持つ対角行列) とおくと、
次のように書けます。
$$
\boldsymbol{\rho}_k = \mathbf{D}^{-1/2} \boldsymbol{\Gamma}_k \mathbf{D}^{-1/2}.
$$

自己相関行列も自己共分散行列と同じように、対角成分は各変数の自己相関になり、
$\boldsymbol{\rho}_k = \boldsymbol{\rho}^{\top}_{-k}$ が成立します。

長くなってきたので一旦記事を切ります。(ベクトルホワイトノイズは次回。)

久しぶりに時系列分析の話題です。
今回はベクトル自己回帰(VAR)モデルを紹介します。
参考書はいつもの沖本先生の経済・ファイナンスデータの計量時系列分析です。
(VARモデルは第4章)

ベクトル自己回帰(VAR)モデルは、自己回帰(AR)モデルをベクトルに一般化したものです。
自然数$p$に対して、ベクトル $\mathbf{y}_t$ を定数(のベクトル)と、自身の$p$期以内の過去の値に回帰したモデルになります。
つまり、次のようなモデルになります。
$$
\mathbf{y}_t = \mathbf{c}+\mathbf{\Phi}_1\mathbf{y}_{t-1}+\cdots+\mathbf{\Phi}_p\mathbf{y}_{t-p}+\mathbf{\varepsilon}_t,
\ \ \ \mathbf{\varepsilon}_t\sim W.N.(\mathbf{\Sigma})
$$
($\mathbf{\varepsilon}$がなぜか太字にならない。自分の環境だけかな。)

ここで、$\mathbf{c}$ は $n\times 1$定数ベクトルで、$\mathbf{\Phi}_i$は$n\times n$行列です。
$\mathbf{\varepsilon}_t$はベクトルホワイトノイズと呼ばれるものです。
(単純に各要素がホワイトノイズのベクトルというわけではありません。このブログでは新出語なので後日別の記事で取り上げます。)

２変量のVAR(1)モデル、要するに実質的なVARモデルとしては一番小さいモデルを具体的に表記すると次のようになります。

$$\left\{\begin{matrix}\
y_{1t} &=&c_1+\phi_{11}y_{1,t-1}+\phi_{12}y_{2,t-1}+\varepsilon_{1t},\\\
y_{2t} &=&c_2+\phi_{21}y_{1,t-1}+\phi_{22}y_{2,t-1}+\varepsilon_{2t}\
\end{matrix}\
\right.\
\left(\begin{matrix}\varepsilon_{1t}\\\varepsilon_{2t}\end{matrix}\right)\sim W.N.(\mathbf{\Sigma})$$

$$
\Sigma = \left(\begin{matrix}\
\sigma_1^2 & \rho\sigma_1\sigma_2\\\
\rho\sigma_1\sigma_2 & \sigma_2^2\
\end{matrix}\right)\
$$

さて、具体的にモデルの形を書き出したのでパラメーターの数を数えてみたいと思います。
回帰式の係数(4個)と定数(2個)で計6個、さらに分散共分散行列部分が3個で、合計9個のパラメーターを持っていることがわかります。

一般的に$n$変数のVAR(p)モデルの場合、
回帰式の定数が$n$個、係数が$n^2p$個で合計$n(np+1)$個、分散共分散行列部分が$n(n+1)/2$個のパラメーターを持ちます。
そのため、比較的大きなモデルになってしまいます。

自分の経験でも、モデルに組み込みたい変数の値の数($n$)は10個も20個もあって、ラグ($p$)は3期くらい前まで見たい、
ということがありましたが、集められたデーターが全然足りず、推定が全然できないということがありました。
(そのときは結局変数をかなり絞り込んだモデルをいくつも作って個別に検証しました。)

さて、ベクトル自己回帰モデルを使う目的ですが、主に二つあります。
一つは、予測の精度向上です。
自己回帰モデルでは、ある値が自身の過去の値で回帰できることこを仮定して予測しますが、
ある値が自分の過去の値以外の外部要因に一切影響を受けない、ということは実用上あまりなく、
大抵は複数の値が相互に関係しているので、複数の種類の値を用いて予測することにより精度の向上が期待できます。

もう一つは、複数の変数間の関係を分析することです。
モデルの形からも明らかなように、それぞれの変数が他の変数にどれだけ寄与しているかをみることができます。

久しぶりに時系列解析の話題です。

以前の記事で、単位根過程という用語を紹介しました。
参考:差分系列と単位根過程
それに関して、見せかけの回帰(spurious regression)という現象があるのでそれを紹介します。

いつもの沖本先生の本から引用します。(127ページ)

定義 (見せかけの回帰)
単位根過程$y_t$を定数と$y_t$と関係のない単位根過程$x_t$に回帰すると、$x_t$と$y_t$の間に有意な関係があり、
回帰の説明力が高いように見える現象は見せかけの回帰と言われる。

この現象を確認するために、実際に単位根過程を2個生成して回帰をやってみましょう。
単位根過程は単純に次の二つのランダムウォークでやります。
それぞれ独立した系列$\varepsilon_{1,t}$と$\varepsilon_{2,t}$から生成しているので、これらは無関係な過程です。
$$
x_t = x_{t-1} + \varepsilon_{1,t} \ \ \ \varepsilon_{1,t}\sim N(0,1)\\
y_t = y_{t-1} + \varepsilon_{2,t} \ \ \ \varepsilon_{2,t}\sim N(0,1)
$$

回帰係数の有意性もみたいので、statsmodelsで実装しました。

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
# データ生成
T = 200
X = np.cumsum(np.random.randn(T)).reshape(-1, 1)
y = np.cumsum(np.random.randn(T))


# 定数項を作成
X0 = sm.add_constant(X)
# 回帰分析実行
st_model = sm.OLS(y, X0)
results = st_model.fit()
#　結果表示
print(results.summary())
'''
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.171
Model:                            OLS   Adj. R-squared:                  0.167
Method:                 Least Squares   F-statistic:                     40.85
Date:                Sat, 25 May 2019   Prob (F-statistic):           1.15e-09
Time:                        23:16:39   Log-Likelihood:                -423.18
No. Observations:                 200   AIC:                             850.4
Df Residuals:                     198   BIC:                             856.9
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -5.2125      0.327    -15.960      0.000      -5.856      -4.568
x1            -0.1826      0.029     -6.391      0.000      -0.239      -0.126
==============================================================================
Omnibus:                        5.521   Durbin-Watson:                   0.215
Prob(Omnibus):                  0.063   Jarque-Bera (JB):                3.122
Skew:                          -0.033   Prob(JB):                        0.210
Kurtosis:                       2.391   Cond. No.                         26.3
==============================================================================
'''

結果を見ると、係数のp値が非常に小さくなっていて、$x_t$と$y_t$の間に関係があるように見えます。

定常過程同士であればこのような現象は発生しないことを見るために、
$x_t$と$y_t$の差分系列をとって、同じように回帰してみましょう。
(差分系列はどちらも定常過程です。)

X_diff = X[1:] - X[:-1]
y_diff = y[1:] - y[:-1]
# 定数項を作成
X0_diff = sm.add_constant(X_diff)
# 回帰分析実行
st_model = sm.OLS(y_diff, X0_diff)
results = st_model.fit()
# 結果表示
print(results.summary())
'''
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.000
Model:                            OLS   Adj. R-squared:                 -0.005
Method:                 Least Squares   F-statistic:                   0.03113
Date:                Sat, 25 May 2019   Prob (F-statistic):              0.860
Time:                        23:48:11   Log-Likelihood:                -265.29
No. Observations:                 199   AIC:                             534.6
Df Residuals:                     197   BIC:                             541.2
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         -0.0195      0.065     -0.298      0.766      -0.148       0.109
x1            -0.0117      0.066     -0.176      0.860      -0.142       0.119
==============================================================================
Omnibus:                        2.378   Durbin-Watson:                   2.107
Prob(Omnibus):                  0.305   Jarque-Bera (JB):                2.338
Skew:                           0.263   Prob(JB):                        0.311
Kurtosis:                       2.923   Cond. No.                         1.01
==============================================================================
'''

p値が明らかにでかい値になりましたね。

今回の記事ではグラフは省略しましたが、
単純にプロットしてみてみると確かに単位根過程同士では何らかの関連を持っているように見え、
定常過程同士では無関係に見えます。

前回に引き続き今回も言葉の定義です。出典はいつもの沖本本から。

和分過程
d-1階差分をとった系列は非定常過程であるが、d階差分をとった系列が定常過程に従う過程は、
d次和分過程、もしくはI(d)過程と呼ばれます。
また、I(0)過程は定常過程で定義されます。

ARIMA過程
d階差分をとった系列が定常かつ反転可能なARMA(p,q)過程に従う過程は、
次数(p,d,q)の自己回帰和分移動平均過程、もしくはARIMA(p,d,q)過程と呼ばれます。

和分過程やARIMA過程の和分次数dは、AR特性方程式におけるz=1という解の個数に等しいことが知られているそうです。

前回の記事で定義した単位根過程は I(1)過程になり、
単位根過程の差分系列が定常で反転可能なARMA(p,q)過程の時、
それはARIMA(p,1,q)過程になります。

単位根過程の例として代表的なものにランダムウォークがあります。
言葉だけなら市場系のデータについて学んでいるとしょっちゅう出てきますね。

過程$y_t$が、
$$
y_t = \delta + y_{t-1} + \varepsilon_t , \ \ \ \varepsilon_t\sim iid(0, \sigma^2)
$$
と表現される時、$y_t$はランダムウォーク(random walk)と呼ばれます。
ただし、 $y_0=0$とします。また、 $\delta$はドリフト率と呼ばれるそうです。

定義式をよく見ると、AR(1)過程の形をしており、
AR特性方程式の解は$1$なので、これが定常でないこともわかります。
また、$\Delta y_t = y_t – y_{t-1} = \delta + \varepsilon_t$
であり、これは定常過程なので、ランダムウォークが単位根過程であることがわかります。

久々に沖本先生の経済・ファイナンスデータの計量時系列分析に戻って、
時系列分析の用語を二つ紹介します。

まずは差分系列(5ページ)。
原系列$y_t$に対して、1点離れたデータとの差を取ることで生成できる系列、$y_t-y_{t-1}$を、
差分系列、または階差系列と呼び、$\Delta y_t$と書きます。

続いて単位根過程(105ページ)。
原系列$y_t$が非定常過程であり、差分系列$\Delta y_t=y_t-y_{t-1}$が定常過程である時、
過程は単位根過程である(unit root process)と言われます。

名前の由来は、単位根過程を誤差項が定常過程であるAR過程を用いて表現した時に、
AR特性方程式が$z=1$という解を１つ持つことらかきているそうです。

単位根過程の定義においては、差分系列が定常過程であることしか定義されておらず、
これがAR過程やARMA過程であることなどは要求されていないので注意です。

(お恥ずかしい話ですが、自分はデータサイエンティストに転職するずいぶん前に時系列分析を雑に勉強して、
差分とったらAR過程になるのが単位根過程だと誤って理解していたことがあります。)

このブログの通常の流れでは、ここから単位根過程のサンプルを一個構築して
プロットした図を出すのですが、実はすでに登場しているのでそちらにリンクしておきます。
参考:自己回帰過程のサンプル
この記事で構築したAR(3)過程の3個目の例が単位根過程です。

前回の記事がMA過程の反転可能性について述べたものだったので、今回はAR過程をMA過程で表現できることについてです。
参考:MA過程の反転可能性

AR過程全てではなく、定常AR過程に限った性質ですが、
定常AR過程はMA($\infty$)過程に書き直すことができます。

たとえば、 $|\phi|<1$の時、次のAR(1)過程は定常です。 $$ y_t = \phi y_{t-1} + \varepsilon_t , \varepsilon_t\sim W.N.(\sigma^2). $$ これは、 $$ y_t = \sum_{k=0}^{\infty}\phi^k\varepsilon_{t-k} $$ と書き直すことができます。 また、MA過程は常に定常なので、MA過程に書きなおせるAR過程は定常です。 ということで、AR過程が定常になる条件と、AR過程をMA過程に書きなおせる条件は同一になり、 AR特性方程式の解を調べることで判断ができます。