カテゴリー: 時系列分析

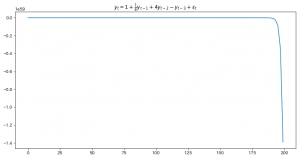
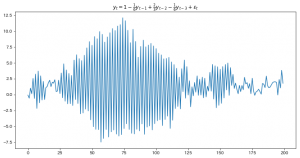
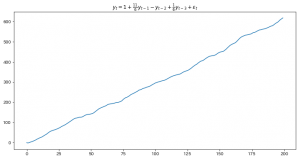
今日もまた沖本本からMA過程の話題です。

本題に入る前にAR過程の復習ですが、このブログでも紹介した通り、
AR過程は定常になるとは限らず、各種の性質については、定常AR過程なら、という前提がついていました。
参考:自己回帰過程の定義と定常になる条件、定常自己回帰過程の性質
その一方で、MA過程については常に定常でなのでとても扱いやすいように見えます。
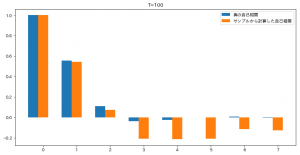
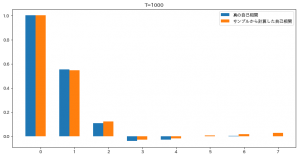
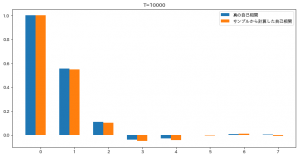
しかし、MA過程には同一の期待値と、同一の自己相関構造を持つ異なるMA過程が複数存在するという問題があります。

一般に、同一の期待値と自己相関構造を持つMA(q)過程は$2^q$個存在するらしいです。
本に、MA(1)の例が載っているので、このブログではMA(4)あたりに対して、この$2^4=16$個がそうだ!って例を見つけて描きたかったのですが、
挫折したので本に載ってるMA(1)に対する例を紹介します。

それは
$$
\begin{eqnarray}
y_t = \varepsilon_t +\theta\varepsilon_{t-1} , \varepsilon_t \sim W.N.(\sigma^2)
\end{eqnarray}
$$
と、
$$
\begin{eqnarray}
y_t = \tilde{\varepsilon}_t+\frac{1}{\theta}\tilde{\varepsilon}_{t-1}, \tilde{\varepsilon}_t \sim W.N.(\theta^2\sigma^2)
\end{eqnarray}
$$
です。
これの期待値や自己相関を 移動平均過程の定義と性質 で紹介した式に沿って計算すると、一致することを確認できます。

この時、$2^q$個のMA(q)過程の中からどれを採用するかの基準が必要になりますが、
そのために一つの基準になるのがMA過程の反転可能性(invertibility)です。

MA(q)過程が反転可能(invertible)とは、そのMA(q)過程をAR($\infty$)過程に書きなおせることです。

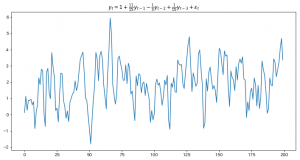
例えば、$|\theta|<1$であれば、 $$ y_t = \varepsilon_t + \theta\varepsilon_{t-1} $$ は $$ y_t = -\sum_{k=1}^{\infty}(-\theta)^ky_{t-k}+\varepsilon_t $$ と書き直せます。 このMA(1)の例も沖本先生の本からです。 (MA(2)の例を紹介しようと計算を頑張っていたのですが思ったより複雑になったので本の例をそのまま。) 一般のMA(q)過程の反転可能性については、AR過程の定常条件とよく似ています。 次のMA特性方程式を調べることで確認できます。 $$ 1+\theta_1z+\theta_2z^2+\cdots+\theta_qz^q=0. $$ このMA特性方程式の全ての解の絶対値が1より大きければMA過程は反転可能になります。 この時、撹乱項$\varepsilon_t$は、$y_t$を過去の値から予測した時の予測誤差と解釈できます。 昔、別の本で移動平均過程を勉強した時、いきなり移動平均もでるは誤差項による回帰だと書かれていて全く理解できなったのですが、 ようやく理解できました。 沖本先生の本だと、反転可能なものの唯一性等の証明が載っていない(そして自分で証明しようともしたが上手くいっていない)ので、 何かの折に他の文献にも当たってみようと思います。

今回も沖本先生の経済・ファイナンスデータの計量時系列分析を元にした記事です。
最近、AR過程やMA過程について色々と紹介していますが、これら両方を含む過程を考えることができます。
それを自己回帰移動平均(ARMA)過程と言います。
(autoregressive moving average process)

(p,q)次ARMA過程(ARMA(p,q)過程)は、次の式で定義されます.

$$
y_t = c + \phi_1y_{t-1}+\cdots+\phi_py_{t-p}+\varepsilon_t+\theta_1\varepsilon_{t-1}+\cdots+\theta_q\varepsilon_{t-q}\\
\varepsilon_t \sim W.N.(\sigma^2)
$$
ARMA過程の性質は、AR過程の性質とMA過程の性質の強い方が残ります。
例えば定常性については、AR過程部分が定常であれば定常になります。
(結果だけ見れば、MA過程が定常過程なので、それに定常過程を足しても定常というだけの話に見えますが、
正確な証明にはもう少し細かな議論を要します)

AR過程部分の定常性については、以前の記事でも紹介したAR特性方程式を使います。

ARMA(p,q)過程が定常の時、過程の期待値は、AR過程部分の期待値と等しくなります。
$$
\mu = E(y_t) = \frac{c}{1-\phi_1-\phi_2-\cdots-\phi_p}
$$

また、$q+1$次以降の自己共分散と自己相関もAR部分とおなじ、次のユール・ウォーカー方程式に従います。
$$
\begin{eqnarray}
\gamma_k & = \phi_1\gamma_{k-1}+\phi_2\gamma_{k-2}+\cdots+\phi_p\gamma_{k-p}, k\geq q+1\\
\rho_k & = \phi_1\rho_{k-1}+\phi_2\rho_{k-2}+\cdots+\phi_p\rho_{k-p}, k\geq q+1
\end{eqnarray}
$$
$q$次までについては、MA項の影響もあり具体的な表記が難しくなります。

また、定常ARMA過程の自己相関は指数的に減衰します。これもAR部分の性質ですね。
(MA過程の部分の自己相関はq+1次以降消えます。)

前回の記事で定常AR過程の自己相関係数を解析的に算出しました。
また、さらに以前の記事で、同じAR(3)過程に従う系列をpythonで生成しています。
このAR(3)過程のサンプルから、自己相関係数を計算したら、それは本当にユール・ウォーカー方程式から求めた値と一致するのかなというのが今回のテーマです。
結論を先に言っておくと非常に長い系列サンプルを用意しないと無理です。

では早速やってみましょう。
今回もサンプルはこれ。(適当に作った系列ですが、このブログでは高頻度で登場します。)

$$
y_t=1+\frac{11}{15}y_{t-1}-\frac{1}{3}y_{t-2}+\frac{1}{15}y_{t-3}+\varepsilon_t , \varepsilon_t \sim iid N(0,\sigma^2)
$$
ユール・ウォーカー方程式から求まる自己相関$\rho_k$の最初の8項は次のようになります。
$$
\begin{eqnarray}
\rho_0 &=& 1.0 \\
\rho_1 &=& 0.5555555555555556 \\
\rho_2 &=& 0.1111111111111111 \\
\rho_3 &=& -0.037037037037037035 \\
\rho_4 &=& -0.027160493827160487 \\
\rho_5 &=& -0.0001646090534979357 \\
\rho_6 &=& 0.006463648834019207 \\
\rho_7 &=& 0.0029841792409693643
\end{eqnarray}
$$

あとは、早速乱数で{y_t}を生成して、pandasの関数で自己相関を算出し、
上の値と比べてみましょう。

まず、100項算出してやってみたのが次のコードです。
注意点として、今回は系列の最初の方のデータを系列の期待値+撹乱項で生成しました。
また、撹乱項の標準偏差を$0.1$にしています。(つまり分散は$0.01$)。
これまで、$1$を使っていましたが、期待値が$1.875$の系列に対する撹乱項としてはちょっと分散が大きすぎましたので。

コードと出力はこちら。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

phi_1 = 11/15
phi_2 = -1/3
phi_3 = 1/15

# 過程の期待値
Ey = 1/(1-phi_1-phi_2-phi_3)

# 項数
T = 100

# 過程の生成
y = np.zeros(T)
# 初期値 (過程の期待値+乱数)
y[0] = Ey + np.random.normal(loc=0, scale=0.1)
y[1] = Ey + np.random.normal(loc=0, scale=0.1)
y[2] = Ey + np.random.normal(loc=0, scale=0.1)
for i in range(3, T):
    y[i] = 1 + phi_1*y[i-1] + phi_2*y[i-2] + phi_3*y[i-3] +\
                np.random.normal(loc=0, scale=0.1)

# 自己相関の算出
series = pd.Series(y)
series_autocorr = [series.autocorr(i) for i in range(8)]


# rho_values に、前回の記事で算出した自己相関が代入されている想定
# 可視化
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1, title='T=100')
ax.bar(np.arange(len(rho_values))-0.3, rho_values,  width=0.3, label='真の自己相関')
ax.bar(range(len(series_autocorr)), series_autocorr, width=0.3, label='サンプルから計算した自己相関')
ax.legend()
plt.show()

ラグが３以上になると全然ダメですね。

Tの値を 1000,10000 と増やして順に実行したのがこちらです。

徐々に近づいてきたようにみます。

自己相関はpandasで結構手軽に計算できるので、
過去にも、時系列データをみたらとりあえず計算して眺めたりしていたのですが、
データ数がかなり大きくないとなかなか真の値に近いものにならないことがわかりました。
そもそも現実データには大量のノイズが入るので、ほんの数年分の
月次データ6ヶ月ラグとかみてもほとんどあてにならなさそうですね。

今回は移動平均過程の例をいくつか生成して紹介します。
$AR(1)$や$AR(2)$の例は色々なところで取り上げられているので、すべて$AR(3)$にしました。

AR特性方程式の解の絶対値が全て1より大きい定常な例を一つと、そうではない例が3つです。
定常ではない例は、AR特性方程式の解に絶対値が$1$より小さなものを含むものと、
$-1$を解に持つもの、$1$を解に持つものを選びました。
なお、撹乱項の分散は$1$に揃えています。
$$\varepsilon_t \sim iid N(0,1)$$

定常なAR(3)過程の例

まずは、次のAR(3)過程を取り扱います。
$$y_t=1+\frac{11}{15}y_{t-1}-\frac{1}{3}y_{t-2}+\frac{1}{15}y_{t-3}+\varepsilon_t$$
AR特性方程式の解は $3,1+2i,1-2i$の3個です。(意図的に虚数解を含むものを選びました。)
解の絶対値が全部1より大きいので、この過程は定常になるはずです。
pythonで時系列データを生成しプロットして見ます。

import sympy
import numpy as np
import matplotlib.pyplot as plt

phi_1 = 11/15
phi_2 = -1/3
phi_3 = 1/15

# 根の確認
z = sympy.symbols('z')
print(sympy.solve(1-phi_1*z-phi_2*z**2-phi_3*z**3))

# 過程の生成
y = np.zeros(200)
# 初期値
y[0] = np.random.randn()
y[1] = np.random.randn()
y[2] = np.random.randn()
for i in range(3, 200):
    y[i] = 1 + phi_1*y[i-1] + phi_2*y[i-2] + phi_3*y[i-3]  + np.random.randn()


fig = plt.figure(figsize=(12, 6))
title = '$y_t=1+\\frac{11}{15}y_{t-1}-\\frac{1}{3}y_{t-2}+\\frac{1}{15}y_{t-3}+\\varepsilon_t$'
ax = fig.add_subplot(1, 1, 1, title=title)
ax.plot(y)
plt.show()

出力がこちら。

いかにも定常な感じですね。

定常ではないAR(3)過程の例 1

次は定常ではないAR(3)過程の例としてこれを考えます。
$$y_t=1+\frac{1}{4}y_{t-1}+4y_{t-2}-y_{t-3}+\varepsilon_t$$
AR特性方程式の解は $-0.5,0.5,4$ であり、絶対値が1より小さいものを含みます。

コードは省略しますが、試しに出力したのがこちら。
撹乱項の値によって形が全然変わるので実行するたびに プラスに振れるのかマイナスに振れるのかも違います。

どう見ても定常ではありませんね。$t$が小さい時と大きい時の$y_t$の期待値が全く違います。

定常ではないAR(3)過程の例 2

もう一つ定常ではないAR(3)過程の例。
今度はAR特性方程式が$-1$を解に持ちます。
$$y_t=1-\frac{1}{6}y_{t-1}+\frac{2}{3}y_{t-2}-\frac{1}{6}y_{t-3}+\varepsilon_t$$

プロットしたのがこちら。

一見定常っぽくも見えますが、非常にギザギザしています。
実はこの過程、奇数番目と偶数番目の項の期待値が違います。
(撹乱項を取り払うと2つの値が交互に現れるので確認しやすいです)
このため、たしかに定常でないことがわかりました。

定常ではないAR(3)過程の例 3

次も定常ではない例ですが、今回はAR特性方程式が、$1$を解に持ちます。
$$y_t=1+\frac{11}{6}y_{t-1}-y_{t-2}+\frac{1}{6}y_{t-3}+\varepsilon_t$$
実はこの過程は定常ではないのですが、差分系列$\Delta y_t=y_t-y_{t-1}$は定常過程になります。
このような過程を単位根過程と言います。
単位根過程の詳しい話はそのうち紹介したいですがとりあえずグラフを出すと次のようになります。

綺麗なトレンドが出ましたね。

例によって沖本本を参照し、自己回帰過程を紹介します。

自己回帰(AR)過程(autoregressive process)は、過程が自分の過去に回帰された形で表現される過程です。
p次AR過程(AR(p)過程)は、次で定義されます。
$$
y_t = c + \phi_1y_{t-1} + \phi_2y_{t-2} + \cdots + \phi_py_{t-p} + \varepsilon_t ,\ \
\varepsilon_t \sim W.N.(\sigma^2)
$$

要するに$y_t$を過去p期間の値に回帰したモデルです。
AR(p)過程は常に定常になるとは限りません。

AR(p)過程が定常になるかどうかは次の方法で確認することができます。
まず、次の変数zの方程式を考えます。 ($\phi_t$は上の定義で登場した係数)
$$
1-\phi_1z-\phi_2z^2-\cdots-\phi_pz^p = 0
$$
これはAR特性方程式とよばれます。また、左辺の多項式はAR多項式と呼ばれるそうです。
この方程式の全ての解の絶対値が1より大きい時、AR過程は定常になります。

AR過程が定常な場合、下記の性質が成り立ちます。
(改めてですが、AR過程は定常でないこともあるので注意です。)

$$
\begin{eqnarray}
\mu & = E(y_t) = \frac{c}{1-\phi_1-\phi_2-\cdots-\phi_p}\\
\gamma_0 & = Var(y_t) = \frac{\sigma^2}{1-\phi_1\rho_1-\phi_2\rho_2-\cdots-\phi_p\rho_p}\\
\gamma_k & = \phi_1\gamma_{k-1}+\phi_2\gamma_{k-2}+\cdots+\phi_p\gamma_{k-p}, k\geq1\\
\rho_k & = \phi_1\rho_{k-1}+\phi_2\rho_{k-2}+\cdots+\phi_p\rho_{k-p}, k\geq1
\end{eqnarray}
$$
そして、AR過程の自己相関は指数的に減衰します。

今回も出典は沖本先生の経済・ファイナンスデータの計量時系列分析から。

ホワイトノイズの線形和で表される過程を移動平均過程(moving average process)と呼びます。
$q$を1以上の整数ととすると、q次移動平均過程$MA(q)$は次で定義されます。
$$y_t=\mu+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+\cdots+\theta_q\varepsilon_{t-q},\ \ \varepsilon_t\sim W.N.(\sigma^2)$$

そして、$y_t$が$MA(q)$過程に従うことを $y_t\sim MA(q)$と書きます。
$MA(q)$過程は常に定常であり、さらに次の性質を持ちます。

$$
\begin{align}
E(y_t) &= \mu\\
\gamma_0 &= Var(y_t) = (1+\theta_1^2++\theta_2^2+\cdots+\theta_q^2)\sigma^2\\
\gamma_k & = \left\{
\begin{matrix}
\ (\theta_k+\theta_1\theta_{k+1}+\cdots+\theta_{q-k}\theta_{q})\sigma^2, & (1\leq k \leq q)\\
0,& (k\geq q+1)
\end{matrix}
\right.\\
\rho_k & = \left\{
\begin{matrix}
\frac{\theta_k+\theta_1\theta_{k+1}+\cdots+\theta_{q-k}\theta_{q}}
{1+\theta_1^2++\theta_2^2+\cdots+\theta_q^2} , & (1\leq k \leq q)\\
0,& (k\geq q+1)
\end{matrix}
\right.
\end{align}
$$
式から分かる通り、MA(q)過程の q+1次以降の自己相関は常に0になります。
そのため、長期間にわたる自己相関を移動平均過程でモデル化するには多くのパラメーターが必要になります。

前回の記事で定義した定常過程の例を紹介します。
(今回も沖本本からの引用です。)

iid系列

iid系列は、強定常過程の例です。

定義:
各時点のデータが互いに独立でかつ同一の分布に従う系列はiid系列と呼ばれる。

iidとは、 independent and identically distributedの略です。
Wikipedia : 同時独立分布

$y_t$が期待値$\mu$,分散$\sigma^2$のiid系列であることを $y_t\sim iid(\mu,\sigma^2)$と書きます。

ホワイトノイズ

独立性や同一分布性は非常に強い仮定なのですが、
実用上、モデルの錯乱項などとして使うのであればもう少し弱い仮定で十分です。
そこで次のホワイトノイズというものが使われます。
ホワイトノイズは弱定常過程です。

定義:
すべての時点$t$において
$$
\begin{align}
E(\varepsilon _t) &=0\\
\gamma _k &= E(\varepsilon _t \varepsilon _{t-k}) =\left\{
\begin{array}{ll}
\sigma^2, & (k=0)\\
0, & (k\neq 0)
\end{array}\right.
\end{align}
$$
が成立するとき, $\varepsilon _t$はホワイトノイズ(white noise)と呼ばれる.

$\varepsilon _t$が分散$\sigma^2$のホワイトノイズであることを $\varepsilon _t\sim W.N.(\sigma^2)$と書きます。
次のようにホワイトノイズを使って、基礎的な弱定常過程の例を作れます。
$$
y_t = \mu + \varepsilon _t,\ \ \ \varepsilon _t\sim W.N.(\sigma^2)
$$

自分だけかもしれないのですが、ホワイトノイズと聞くと無意識に$(\varepsilon _t,\cdots,\varepsilon _{t+k})$の同時分布が期待値0の多変量正規分布であるかのようにイメージしてしまいます。
しかし定義の通り、ホワイトノイズにはそこまでの強い仮定はないので注意です。

ちなみに $(y_t,\cdots,y_{t+k})$の同時分布が多変量正規分布の場合、それは正規過程と呼ばれ、
正規過程に従うホワイトノイズは正規ホワイトノイズと呼ばれます。(沖本本のp9,p12)
正規ホワイトノイズはiid過程なので、強定常過程になります。