今回紹介するのは階層型クラスタリングをscipyで実施する方法です。
階層型クラスタリングの各種アルゴリズム自体は、まだエンジニアを本職にしてたころに知り、その時はこれは面白い手法だと感心していたのですが、
いざデータサイエンティストに転職してからはあまり使ってきませんでした。
クラスタリングする時はk-meansなど、クラスタ数を指定する手法を使うことが多いし、
どれとどれが近いとか言った分析は距離行列眺めたり、次元削減してプロットしたりすることが多かったので。
ただ、他の職種のメンバーに説明するときの樹形図(デンドログラム)のわかりやすさを活用したくなり最近使い始めています
さて、本題に戻ります。
階層型クラスタリングを雑に説明すると、一旦個々のデータを全部別々のクラスタに分類し、
その中から近いものを順番に一つのクラスタにまとめるという操作を繰り返し、最終的に全データを1個のクラスタにまとめる方法です。
この操作を途中で打ち切ることで、任意の個数のクラスタにここのデータを分類することができます。
この際、個々の要素の距離をどう定義するのか、またクラスタと要素、クラスタとクラスタの距離をどのように定義するかによって、
手法が複数存在し、結果も変わります。
この階層型クラスタリングを行う関数が、scipyに用意されています。
Hierarchical clustering (scipy.cluster.hierarchy)
非常に多くの関数がありますが使うのは次の3つです。
scipy.cluster.hierarchy.linkage ・・・ 主役。これが階層型クラスタリングの実装。
scipy.cluster.hierarchy.fcluster ・・・ 各要素について、クラスタリングの結果どのクラスタに属するのかを取得する。
scipy.cluster.hierarchy.dendrogram ・・・ 樹形図(デンドログラム)を描く。
ここまで読んであまりイメージがつかめないと思うので、とりあえずやってみましょう。
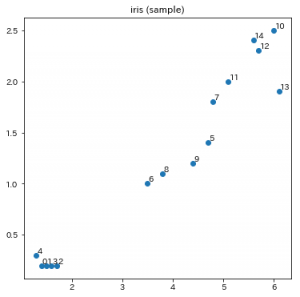
データは何でもいいのですが、いつものirisでやります。
(そんなに多くの件数も必要ないので、1/10の件数のデータに絞って使い、4つある特徴量のうち2個だけ使います)
# データ取得。 (15件だけ取得し、特徴量も petal lengthとpetal width に絞る
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
X = load_iris().data[::10, 2:4]
# データを可視化。
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1, title="iris (sample)")
plt.scatter(X[:, 0], X[:, 1])
for i, element in enumerate(X):
plt.text(element[0]+0.02, element[1]+0.02, i)
plt.show()
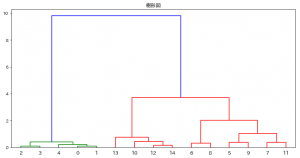
出力がこちら。これをクラスタリングしていきます。
散布図には番号を振っておきましたが、この番号が結果に出てくる樹形図(デンドログラム)内の番号に対応します。
つぎに階層型クラスタリングを実行して可視化します。
# 階層型クラスタリングに使用する関数インポート
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
# ユークリッド距離とウォード法を使用してクラスタリング
z = linkage(X, metric='euclidean', method='ward')
# 結果を可視化
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1, title="樹形図")
dendrogram(z)
plt.show()
0,1,2,3,4 が早い段階で一つのクラスタにまとまっていたり、 12と14、6と8が早々にまとまっていたりと納得性のある形になっています。
あとは、もっと扱いやすい形で、何番のデータが何番目のクラスタに所属するのかのリストを作りましょう。
ここで fcluster 関数を使います。
詳しくはドキュメントにありますが、 criterion に ‘maxclust’を指定して、最大クラスタ数で決めたり、
criterion に’distance’ を指定して、距離で閾値を指定したりできます。
ドキュメントを読むよりやってみたほうがわかりやすいと思うのでそれぞれやってみます。
(この辺の話は専用に別記事を用意して取り上げるかも。)
from scipy.cluster.hierarchy import fcluster
# クラスタ数を指定してクラスタリング
clusters = fcluster(z, t=3, criterion='maxclust')
for i, c in enumerate(clusters):
print(i, c)
# 以下出力
0 1
1 1
2 1
3 1
4 1
5 3
6 3
7 3
8 3
9 3
10 2
11 3
12 2
13 2
14 2
0,1,2,3,4 と 5,6,7,8,9,11 と 10,12,13,14 の3グループにきちんと別れました。
この他、樹形樹に横線を引いてその位置で分けることもできます。
距離=3くらいで分ければ同じ3グループに分かれるのですが、せっかくなので別のところで切りましょう。
距離=1.7を閾値にして、4グループに分かれるのを確認します。
# 距離の閾値を決めてクラスタリング
clusters1 = fcluster(z, 1.7, criterion='distance')
for i, c in enumerate(clusters1):
print(i, c)
# 以下出力
0 1
1 1
2 1
3 1
4 1
5 4
6 3
7 4
8 3
9 4
10 2
11 4
12 2
13 2
14 2
クラスタ1や、クラスタ2は先ほどと同じですが、6,8 と 5,7,9,11 が別のクラスタに別れました。
これらが分かれる理由は上の樹形図を見ていただければ理解できると思います。