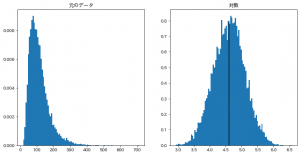
そもそも、Tableauなどを使えばこんな手間もないのですが、Python(Matplotlib)でヒストグラムを描く時に、各ビンの区間を指定したいことがよくあります。
0かはじめて0.5区切りにしたいとか20区切りにしたいとかです。
Matplotlibのhistメソッドでは、bins引数で、binの引数を指定でき、range引数でヒストグラムに描写する幅を指定できるので、
僕はこれまではこの二つを組み合わせて使うことで、想定通りのヒストグラムを描いていました。
試しに、 0 〜 300のデータを 20区切りで、15本のbinでヒストグラムに表示するコードがこれです。
hist メソッドの戻り値で binの区切り位置が取れるので、そちらを確認し、出力の図は省略します。
参考: matplotlibのhist()の戻り値
import matplotlib.pyplot as plt
from scipy.stats import beta
# データ生成
beta_frozen = beta(a=1, b=1, scale=300)
data = beta_frozen.rvs(100)
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
ns, bins, _ = ax.hist(data, bins=15, range=(0, 300))
print(bins)
# [ 0. 20. 40. 60. 80. 100. 120. 140. 160. 180. 200. 220. 240. 260. 280. 300.]
これ、もしreangeを指定せずに、bins=15だけ指定しているととても中途半端なところで区切られます。
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
ns, bins, _ = ax.hist(data, bins=15)
print(bins)
"""
[ 0.59033775 20.53472376 40.47910977 60.42349579 80.3678818
100.31226782 120.25665383 140.20103985 160.14542586 180.08981188
200.03419789 219.9785839 239.92296992 259.86735593 279.81174195
299.75612796]
"""
さて、上記のようなblog記事ように自分で生成したデータなど取りうるレンジがわかりきってるものであれば、上記のやり方でも問題なのですが、実データでは少しだけ面倒です。
レンジとデータ量を確認して、何本くらいのbinを指定すれば切りの良い区切りで可視化でできるか考えないといけません。
しかしドキュメントあたらめて読んでみると、bins引数で、ビンの本数ではなく、区間を配列で指定できることがわかりました。
参考: matplotlib.pyplot.hist
bins : int or sequence or str, optional
If an integer is given, bins + 1 bin edges are calculated and returned, consistent with numpy.histogram.
If bins is a sequence, gives bin edges, including left edge of first bin and right edge of last bin. In this case, bins is returned unmodified.
これを使うと、例えば20区切りで可視化したい、と言った時は次のような書き方ができます。
# 300を含めるため、2個目の引数は301にしました。
bins = range(0, 301, 20)
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
ns, bins, _ = ax.hist(data, bins=bins)
print(bins)
# [ 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300]
楽ですね。
注意点として、 bisで渡した配列の区間の外側のデータは可視化されないということがあります。
bins = range(0, 300, 20) とすると、binsの配列は、
[ 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280]
になるので、 280~300のデータは可視化されません。
区間の下側も同様です。
なので、binsを指定する時に、データが全部その範囲に含まれているのかは確認しておく必要があります。
ちなみに豆知識ですが、各区間は最後(最大)の区間以外は、左の値を含み右の値を含みません、
[20, 40) の区間であれば、 $20 \leq x < 40$ のデータを数えます。
ただし、最後(最大)の区間に限って、右の値も含み、最大のbinが
[280, 300] の区間であれば、 $280 \leq x \leq 300$ のデータを数えます。
使いどこがすぐには思いつかないのですが、 bins を配列で指定する場合は、等間隔以外の区切りもサポートされているということも覚えておきましょう。