前々回の記事の中で例として挙げたモデルの中でガンマ分布を使ったのですが、そういえばガンマ分布を久しぶりに使ったなぁと思ったのでこの機会にその定義や性質等をまとめておこおうと思います。
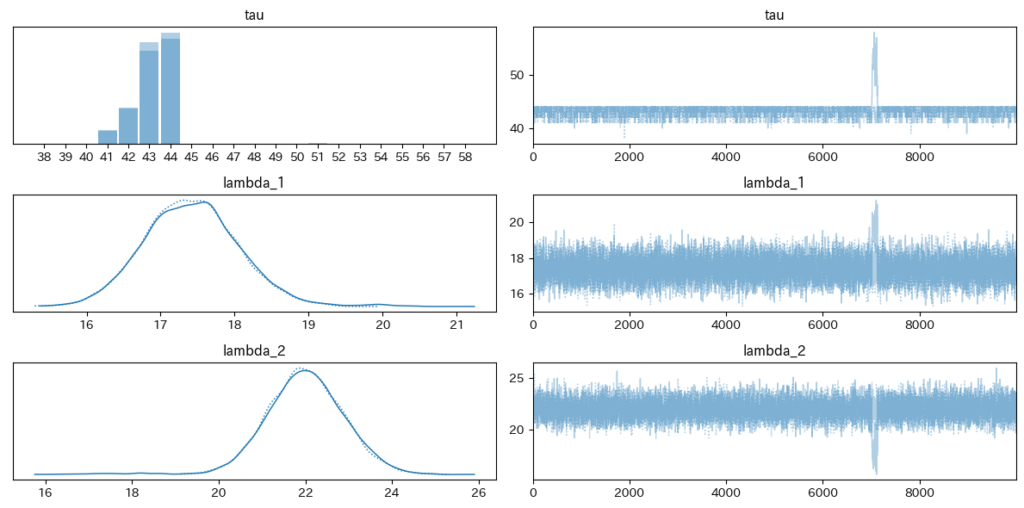
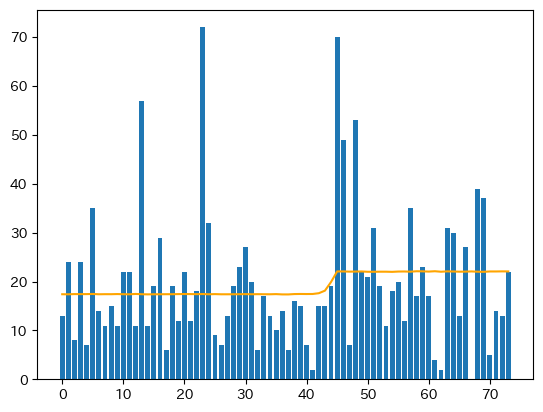
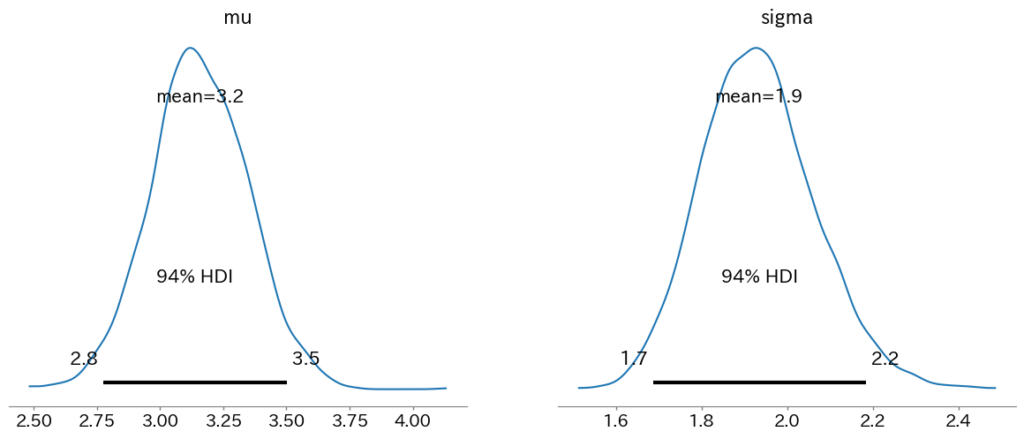
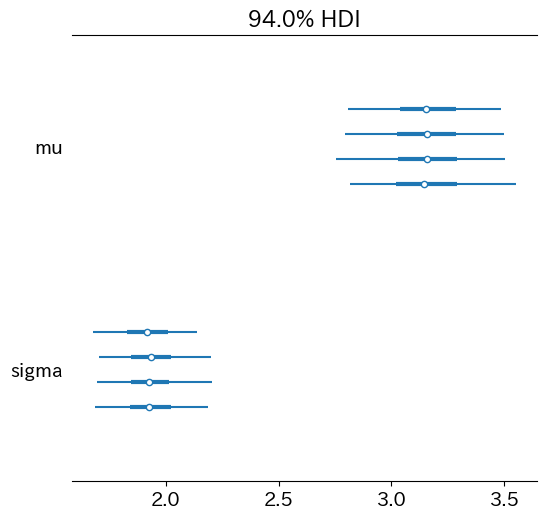
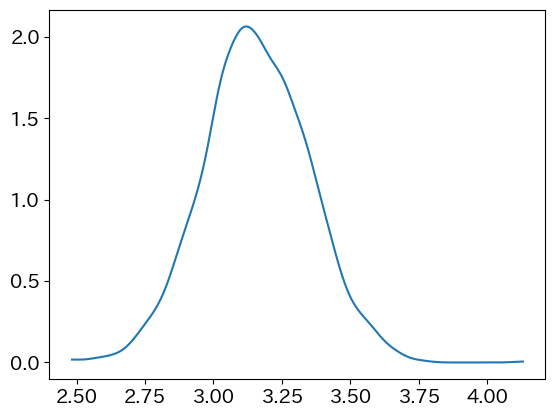
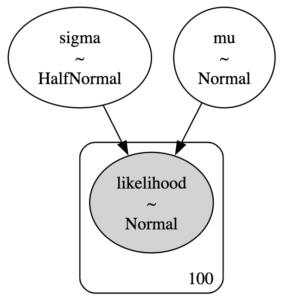
参考: pyMCで変化点検出 (事前分布としてガンマ分布を採用しました)
まず、ガンマ分布の名前の由来になっているのがガンマ関数なので先にその定義も書いておきます。ガンマ関数は実部が正の複素数$z$に対して次の積分で定義される関数です。ちなみに解析接続して、一般の複素数に対しても定義されます。
$$
\Gamma(z) = \int_{0}^{\infty} t^{z-1}e^{-t}dt.
$$
このガンマ関数は、$$\Gamma(n+1) = n!$$という極めて重要な関係式が成り立ち、階乗の一般化とみなせます。
本題のガンマ関数ですが、これは形状母数$k>0$と尺度母数$\theta>0$を用いて確率密度関数が次の式で定義される関数です。
$$
f(x) = \frac{1}{\Gamma(k)\theta^k}x^{k-1}e^{-x/\theta} \qquad (x > 0) .
$$
$\theta$の代わりに、$\lambda = \frac{1}{\theta}$を用いて、次のように表現されることもあります。僕は個人的にはこっちの方が好きです。
$$
f(x) = \frac{\lambda^k}{\Gamma(k)}x^{k-1}e^{-\lambda x} \qquad (x > 0) .
$$
期待値と分散は次の式で表されます。後で紹介しますが、指数分布との関係を考慮するととても自然な結果です。
$$
\begin{align}
E(X)&=k\theta&=\frac{k}{\lambda}\\
V(X)&=k\theta^2&=\frac{k}{\lambda^2}\\
\end{align}
$$
他の確率分布との関係
ガンマ分布はさまざまな分布との関係が深い確率分布です。特に基本的なものを紹介します。
まず、ガンマ分布の$k$が整数の場合に特別な名前がついていて、これをアーラン分布と言います。ガンマ関数を階乗として書けますので、次の形になりますね。
$$f(x) = \frac{1}{(k-1)!\theta^k}x^{k-1}e^{-x/\theta} \qquad (x > 0) .$$
個人的に重要だと考えているのは、互いに独立で同一の指数分布に従う$k$個の確率変数の和は形状母数$k$のガンマ分布に従うことです。個数$k$は明らかに整数なのでこれは正確にはアーラン分布の性質なのですが、ガンマ分布の特徴と考えても良いでしょう。
逆にガンマ分布において$k=1$とすると、ただの指数分布になります。
指数分布についてはこのブログでも過去に紹介しています。
参考: 指数分布について
その記事で紹介した指数分布の期待値と分散を考慮すると、ガンマ分布の期待値と分散がちょうど$k$倍になるのは納得ですね。
もう一つ、1以上の整数$n$に対して、$k=\frac{n}{2}$かつ$\theta=2$とすると、ガンマ分布は自由度$n$のカイ二乗分布になります。
カイ二乗分布もこのブログで紹介しているので確率密度関数の式の形を見比べてみてください。
参考: カイ二乗分布について
そして最後に、ガンマ分布はポアソン分布とも深い関係にあります。ベイズ統計においてはガンマ分布がポアソン分布の共役事前分布になることが特に重要でしょう。
前出の変化点検出のモデルでも、この性質があるのでガンマ分布を事前分布に採用しました。これについては別記事でちゃんと証明をつけたいと思います。