以前(pythonを勉強し始めた頃)は、matplotlibでローソク足をかけたはずなのですが、最近は方法が変わってしまったようなのでそのメモです。
なお、ここでサンプルに使うデータはすでにcsvフィアルか何かで保存されているものとします。
以前は matplotlib.finance というのをimport でき、これを使ってかけたのですが、version 2.0 からなくなってしまったようです。
matplotlib.finance
This module is deprecated in 2.0 and has been moved to a module called mpl_finance.
そしてさらに良くないことに、移動先の mpl_finance ですが、あまりしっかり保守されてない様子。
githubのリポジトリに下記の文言があります。
The code is provided as is and is basically un-maintained.
ただ、一応動くようなので動かしてみましょう。
anacondaには含まれていないようなので、インストールから必要です。
pip install mpl_finance
これで、
mpl-finance==0.10.0
が入りました。
さて、使い方ですがun-maintainedの宣言通り、 mpl-finance の公式ドキュメントらしきものは見当たらず、
上の、matplotlib.finance時代のドキュメントを読んで使わないといけないようです。
ローソク足を書く関数は次の4つあり、それぞれデータの渡し方が違います。
.candlestick2_ochl(ax, opens, closes, highs, lows, width=4, colorup=’k’, colordown=’r’, alpha=0.75)
.candlestick2_ohlc(ax, opens, highs, lows, closes, width=4, colorup=’k’, colordown=’r’, alpha=0.75)
.candlestick_ochl(ax, quotes, width=0.2, colorup=’k’, colordown=’r’, alpha=1.0)
.candlestick_ohlc(ax, quotes, width=0.2, colorup=’k’, colordown=’r’, alpha=1.0)
今回は手元のデータと相性が良いので .candlestick_ohlc を使います。
quotes に 日付、始値、高値、安値、終値、の5列のデータがデータ件数行だけ並んだ配列を渡してあげる必要があります。
ここで面倒なのは日付の渡し方で、float型で渡す必要があります。
ドキュメントに time must be in float days format – see date2num
とある通り、専用の関数があるのでそれを使います。
matplotlib.dates.date2num(d)
また、この関数は引数がdatetime型なので、元々が2019-05-07 のような文字列になっているならば、
datetime型に変換しておく必要があります。
それにはpandasの to_datetimeを使います。
pandas.to_datetime
(いつもならそれぞれ1記事使ってるようなテクニックですね。to_datetimeの方は便利なのでそのうち専用記事書くかも。)
前置きが長くなりましたが、ここまでの情報でできるので日経平均のcsvデータからローソク足を書いてみましょう。
import pandas as pd
import mpl_finance
import matplotlib.pyplot as plt
from matplotlib.dates import date2num
# データの読み込み
df = pd.read_csv("./日経平均データ.csv")
print(df.head())
'''
date open high low close
0 2019-3-11 21062.75 21145.94 20938.00 21125.09
1 2019-3-12 21361.61 21568.48 21348.81 21503.69
2 2019-3-13 21425.77 21474.17 21198.99 21290.24
3 2019-3-14 21474.58 21522.75 21287.02 21287.02
4 2019-3-15 21376.73 21521.68 21374.85 21450.85
'''
# dateの型変換
# まずdatetime型にする
print(df["date"].dtypes) # object
df["date"] = pd.to_datetime(df["date"])
print(df["date"].dtypes) # datetime64[ns]
# 続いて float型へ
df["date"] = matplotlib.dates.date2num(df["date"])
print(df["date"].dtypes) # float64
print(df.head())
'''
date open high low close
0 737129.0 21062.75 21145.94 20938.00 21125.09
1 737130.0 21361.61 21568.48 21348.81 21503.69
2 737131.0 21425.77 21474.17 21198.99 21290.24
3 737132.0 21474.58 21522.75 21287.02 21287.02
4 737133.0 21376.73 21521.68 21374.85 21450.85
'''
# 可視化
fig = plt.figure(figsize=(13, 7))
ax = fig.add_subplot(1, 1, 1)
mpl_finance.candlestick_ohlc(ax, df.values)
plt.show()
こうして出来上がるチャートが次です。
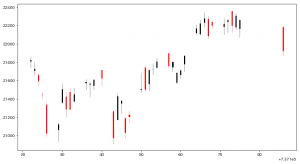
正直これ単体では手間の割に可視化するメリットがないなーというのが正直なところです。
ただ、matplotlibの仕組みに乗っかっているので、
自分のオリジナルの指標などを追加していくことができます。