時系列解析で理論の話題が続いていましたが、用語の定義がだいぶ済んだので、
そろそろ実際にコードを書いてモデルの推定等をやってみます。
(とはいえAIC,BICなどのかなり重要なキーワードや、推定の理論面の話をまだ紹介してないのですが。)
今回はAR(2)過程のデータを生成し、statusmodelsを使って、そのパラメーターを推定します。
真のモデルが不明なサンプルデータではなくてもともと正解がわかってるデータで雰囲気をつかもうというのが主目的です。
今回使うのは、次の定常AR(2)過程です。
$$
y_t = 5 + 1.4y_{t-1} – 0.48y_{t-2} + \varepsilon_{t}, \ \ \varepsilon_{t} \sim W.N.(0.5^2)
$$
早速データを生成して可視化しておきましょう。(過去の記事の例と大して変わらないので、可視化の結果は略します。)
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np
phi_1 = 1.4
phi_2 = -0.48
c = 5
sigma = 0.5
T = 500
# 過程の期待値
mu = c/(1-phi_1-phi_2)
# データの生成
ar_data = np.zeros(T)
ar_data[0] = mu + np.random.normal(0, sigma)
ar_data[1] = mu + np.random.normal(0, sigma)
for t in range(2, T):
ar_data[t] = c + phi_1*ar_data[t-1] + phi_2*ar_data[t-2] \
+ np.random.normal(0, sigma)
# データの可視化 (記事中では出力は略します)
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1)
ax.plot(ar_data)
plt.show()
あとはこのデータから、元のパラメータである、定数項の5や、自己回帰係数の1.4と-0.48、撹乱項の分散0.25(=0.5^2)などを
推定できれば成功です。
使うのはこれ。
statsmodels.tsa.ar_model.AR
fitの戻り値であるARResultsのドキュメントも読んでおきましょう。
statsmodels.tsa.ar_model.ARResults
早速やってみます。
なお、手順は以下の通りです。
- ARモデルの生成
- 次数の決定(select_order, 今回はAICを使用)
- 決定した次数で推定
- 推定結果の確認
# モデルの生成
model = sm.tsa.AR(ar_data)
# AICでモデルの次数を選択
print(model.select_order(maxlag=6, ic='aic')) # 出力:2
# 推定
result = model.fit(maxlag=2)
# モデルが推定したパラメーター
print(result.params)
# 出力
# [ 5.68403723 1.38825575 -0.47929503]
print(result.sigma2)
# 出力
# 0.23797695866882768
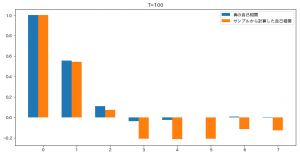
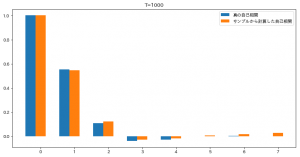
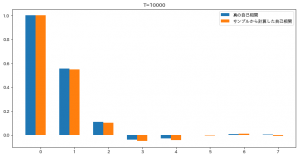
今回は正解にそこそこ近い結果を得ることができました。
乱数を使うので当然ですが実行するたびに結果は変わります。
また、T=500くらいのデータ量だと、モデルの次数が異なる値になることも多く、
結構上手くいかないことがあります。
実行するたびに全然結果が変わるのと、
実際の運用では同一条件のデータを500件も集められることは滅多にないので、
正直、ARモデルでの推定結果をあまり過信しすぎないように気をつけようと思いました。