前回の記事の二分法に続いて、もう一つ求根アルゴリズムを紹介します。
参考: 二分法を用いて関数の根を求める
今回紹介するのはニュートン法です。これは微分可能な関数$f(x)$の根を求めることができるアルゴリズムです。
参考: ニュートン法 – Wikipedia
詳しい説明は上記のWikipediaにあるので、ざっくりと概要を説明します。
この方法の背景にあるのは、滑らかな関数をある点の近くだけ着目してみるとほぼ直線になり、接線で近似できるということをベースのアイデアにしています。
つまり、微分可能な関数$f$があって$f(x)=0$だとします。その根$x$の近くに点$x_0$を取ると、$x_0$の近くでは、$f$と$f$の接線ってかなり近いよね、それなら$f$の根と$f$の$x_0$における接線の根って近いよね、っていうのが基本的なアイデアです。
関数$f$の$f(x_0)$における接戦は次の式で書けます。
$$y=f'(x_0)(x-x_0)+f(x_0).$$
$f(x)=0$は解けない場合でも、この接線の根は容易に算出することができ、
$$x_0-\frac{f(x_0)}{f'(x_0)}$$
と求まります。
この値は元の$x_0$よりも真の根に近いことが期待され、これをもう一回$x_0$とおいて同じ操作を繰り返せば真の根にたどり着く、というのがニュートン法です。
Wikipediaから画像拝借しますが、図で見るとイメージしやすいですね。
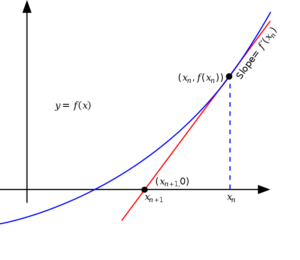
注意しないといけないのは、初期値$x_0$は真の根$x$の十分近くに取らないといけない点です。十分近くを見れば関数をその接線で近侍できるよね、というのがアイデアの前提なので、根が近くになかったらその前提が崩れてしまいこのアルゴリズムは真の根に収束しなくなってしまいます。
ニュートン法のメリットとデメリット
先に紹介した二分法と比べて、ニュートン法のメリットデメリットを説明していきます。
1番のメリットは収束の速さです。二分法に比べてより少ない計算回数で効率的に会を探索することができます。
また、初期値として与える点が1点だけで良いというのもメリットです。二分法の場合は初期値は区間で設定する必要がありましたからね。
その一方で複数のデメリットもあります。実装していて一番不便に感じるのはその関数だけでなく微分も必要ということでしょうか。もちろん微分不可能な関数ではニュートン法は使えません。
また、初期値が真の解に十分近くない場合や、微分した値が$0$に近い場合、うまく収束せずにアルゴリズムが失敗してしまう、という点も大きなデメリットです。
SciPyによる実装
SciPyではscipy.optimizeというモジュールで実装されています。newtonという専用メソッドを使うか、root_scalarという汎用的なメソッドで(method=’newton’)を指定して使うことになります。二分法と同じですね。
参考:
scipy.optimize.newton — SciPy v1.12.0 Manual
root_scalar(method=’newton’) — SciPy v1.12.0 Manual
二分法の時と同じように、$\sin$関数の根$\pi$を探索させてみましょう。微分は$\cos$なのでこれを使います。
from scipy import optimize
import numpy as np
root1 = optimize.newton(np.sin, x0=3, fprime=np.cos)
print(root1)
# 3.141592653589793
root_result = optimize.root_scalar(np.sin, method="newton", x0=3, fprime=np.cos)
print(root_result)
"""
converged: True
flag: 'converged'
function_calls: 6
iterations: 3
root: 3.141592653589793
"""
print(root_result.root)
# 3.141592653589793簡単ですね。
注目するのは、iterationsの部分です。たった3回のイテレーションで収束していて、関数が実行されたのは、fとfの微分合わせて6回だけです。
二分法の時は39回もイテレーションが必要だったのと大違いです。そして実はこの例では解の精度もニュートン法の方が高くなっています。
ニュートン法が失敗する例
初期値が真の解の近くにないと失敗するという話がありましたのでそちらも見ておきます。
例えば、タンジェントの逆関数、$\arctan$で試してみましょう。(sin, cosは根が無限にあって、根から遠い実数を用意できないので関数を変えます。)
$\arctan(x)$の微分は$\frac{1}{1+x^2}$です。
やってみました。
def f(x):
return np.arctan(x)
def fprime(x):
return 1/(1+x**2)
# 初期値が1なら収束する
root_result_1 = optimize.root_scalar(np.sin, method="newton", x0=1, fprime=fprime)
print(root_result_1)
"""
converged: True
flag: 'converged'
function_calls: 12
iterations: 6
root: 0.0
"""
# 初期値が2だと失敗し、結果のflagが'convergence error'になる。
root_result_2 = optimize.root_scalar(np.sin, method="newton", x0=2, fprime=fprime)
print(root_result_2)
"""
converged: False
flag: 'convergence error'
function_calls: 100
iterations: 50
root: 1.854706857103781
"""
# optimize.newton の方だと例外が上がる。
try:
optimize.newton(f, fprime=fprime, x0=2)
except Exception as e:
print(e)
# Derivative was zero. Failed to converge after 10 iterations, value is -6.999943395317963e+168.失敗した時の振る舞いがそれぞれ違うので、どちらのコードを使うかで注意深く扱う必要がありますね。optimize.root_scalarはコード自体は正常に終了しますがフラグが立ち、optimize.newtonの方は例外があがります。
ちなみに、エラーの中で出てくるvalue の値、 -6.999943395317963e+168 は次のように自分でニュートン法を実装しても同じ値が出て来ます。
x0 = 2 # 初期値
for i in range(12):
x0 = x0 - f(x0)/fprime(x0)
print(i+1, "回目: x0=", x0)
"""
1 回目: x0= -3.535743588970453
2 回目: x0= 13.950959086927496
3 回目: x0= -279.34406653361754
4 回目: x0= 122016.9989179547
5 回目: x0= -23386004197.933937
6 回目: x0= 8.590766671950415e+20
7 回目: x0= -1.1592676698907411e+42
8 回目: x0= 2.110995587611039e+84
9 回目: x0= -6.999943395317963e+168
10 回目: x0= inf
11 回目: x0= nan
12 回目: x0= nan
"""絶対値が大きくなり続けていて全く収束に向かっていないのがわかりますね。
まとめ
元の関数だけではなく導関数も必要だったり、初期値の設定段階である程度解の目星をつけておかないといけないなどのデメリットはありますが、速度や精度の面で優秀でしかもロジックもわかりやすい手法なので、何か機会があればニュートン法の活用を検討してみてください。