今回からしばらくカーネル密度推定法について書いていきます。
参考文献ですが「パターン認識と機械学習 上 (PRML 上)」の 119ページ、 2.5.1 カーネル密度推定法 あたりがわかりやすいのではないでしょうか。
ただし、この本だと最後にパラメーター$h$の決め方が重要だ、ってところまで書いて、$h$の決め方を紹介せずに次の話題に移っているので、
これからの数回の記事の中でそこまで説明できたらいいなと思っています。
さて、カーネル密度推定法を大雑把に言うと、
「確率密度が全然わからない確率分布から標本が得られたときに、その標本からできるだけいい感じに元の確率密度を推定する方法」です。
元の確率密度が正規分布だとかポアソン分布だとかだけでもわかっていたら、その期待値や分散などのパラメーターだけ推定すればいい(これをパラメトリックという)のですが、
それさえもわからないときに使われる手法であり、ノンパラメトリックなアプローチと呼ばれます。
できるだけ一般的な形でカーネル密度推定法の方法を書くと次のような形になります。
ある$D$次元のユークリッド空間の未知の確率密度$p(\mathbf{x})$から、観測値の集合$\{\mathbf{x}_n\}\ \ (n=1,2, \cdots, N)$が得られたとします。
そして、次の性質を満たすカーネル関数$k(\mathbf{u})$を選びます。
$$
\begin{align}
k(\mathbf{u}) &\geq 0,\\
\int k(\mathbf{u}) d\mathbf{u} &= 1
\end{align}
$$
このとき、$p(\mathbf{x})$を次で推定するのがカーネル密度推定法です。($h$はパラメーター。)
$$
p(\mathbf{x}) = \frac{1}{N}\sum_{n=1}^{N}\frac{1}{h^D}k(\frac{\mathbf{x}-\mathbf{x}_n}{h}).
$$
カーネル密度関数は要は確率密度間数ですね。理論上は何でもいいそうですが、現実的には原点周りで値が大きく、そこから外れると0に近く(もしくは等しく)なる関数が好都合です。
正規分布の確率密度関数(ガウスカーネル)が頻繁に用いられます。
上記の式が導出されるまでの話はPRMLに書いてあります。
その部分を省略してしまったので代わりに上の定義通り計算して、未知の確率分布が近似できている様子を確認しておきましょう。
できるだけライブラリ使わないでやります。(ただ、正解データの分布作成でscipyは使っていますし、numpyやmatplotlibは例外とします。)
カーネル関数にはガウスカーネルと、単位超立方体内で1、その外で0を取る関数(パルツェン窓というらしい)の2種類でやってみます。
元となる分布は正規分布2個を足した、2つ山のある分布で実験します。($D$は1です)
最初に正解になる分布関数の定義と、そこからのデータサンプリングを済ませておきます。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
# 推定したい分布の真の確率密度関数
def p_pdf(x):
return (norm.pdf(x, loc=-4, scale=2)+norm.pdf(x, loc=2, scale=1))/2
# その分布からのサンプリング
def p_rvs(size=1):
result = []
for _ in range(size):
if norm.rvs() < 0:
result.append(norm.rvs(loc=-4, scale=2))
else:
result.append(norm.rvs(loc=2, scale=1))
return np.array(result)
# グラフ描写のため真の確率密度関数の値を取得しておく
xticks = np.linspace(-10, 5, 151)
pdf_values = p_pdf(xticks)
# 50件のデータをサンプリング
X = p_rvs(50)
そして、それぞれのカーネル関数と、それを使ったカーネル密度関数を定義しておきます。
# パルツェン窓
def parzen_window(u):
if np.abs(u) <= 0.5:
return 1
else:
return 0
# ガウスカーネル
def gaussian_kernel(u):
return(np.exp(-(u**2)/2)/np.sqrt(2*np.pi))
# パルツェン窓を用いたカーネル密度推定
def parzen_kde(x, h, dataset):
return sum([parzen_window((x-d)/h) for d in dataset])/(len(dataset)*h)
# ガウスカーネルを用いたカーネル密度推定
def gaussian_kde(x, h, dataset):
return sum([gaussian_kernel((x-d)/h) for d in dataset])/(len(dataset)*h)
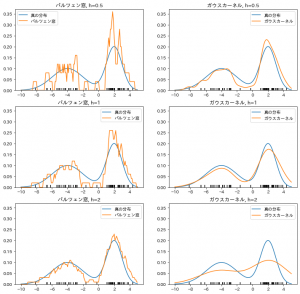
あとは可視化です。 今回は パラメーター$h$は$0.5, 1, 2$の3つ試しました。
fig = plt.figure(figsize=(12, 12), facecolor="w")
# 3種類のhで実験
for i, h in enumerate([0.5, 1, 2]):
parzen_kde_values = [parzen_kde(x, h, X) for x in xticks]
gaussian_kde_values = [gaussian_kde(x, h, X) for x in xticks]
ax = fig.add_subplot(3, 2, i*2+1, facecolor="w")
ax.set_title(f"パルツェン窓, h={h}")
ax.plot(xticks, pdf_values, label="真の分布")
ax.plot(xticks, parzen_kde_values, label="パルツェン窓")
# 標本データ
for x in X:
ax.vlines(x, ymin=0, ymax=0.01)
ax.set_ylim((0, 0.37))
ax.legend()
ax = fig.add_subplot(3, 2, i*2+2, facecolor="w")
ax.set_title(f"ガウスカーネル, h={h}")
ax.plot(xticks, pdf_values, label="真の分布")
ax.plot(xticks, gaussian_kde_values, label="ガウスカーネル")
# 標本データ
for x in X:
ax.vlines(x, ymin=0, ymax=0.01)
ax.set_ylim((0, 0.37))
ax.legend()
plt.show()
出力結果がこれです。
青い線が真の分布、黒くて短い縦線たちが推定に使った標本データ、
オレンジの線が推定した分布です。
「元の確率密度関数の形が全くわからない」という前提から出発している割にはうまく推定できているのもあると言えるのではないでしょうか。
また、カーネル密度関数の選び方、$h$の決め方がそれぞれ重要であることも分かりますね。
やってることといえば、得られた標本の付近で大きめの値を取る関数を全ての標本について計算してその平均を取っているだけなのですが、シンプルな割に強力です。