前回の記事の続きです。
参考: 1標本コルモゴロフ–スミルノフ検定について理解する
コルモゴロフ-スミルノフ検定(K-S検定)は、一つの標本が何かしらの確率分布に従っているかどうかだけではなく、二つの標本について、それらが同一の確率分布から生成されたものかどうかの判定にも利用可能です。
Wikipediaを見ると、KS検定は1標本より2標本の時の利用の方が推されてますね。2標本それぞれの確率分布が不明となるとノンパラメトリックな手法が有効になるのでしょう。
前の記事みたいに数式をつらつらと書いていこうかと思ったのですが、1標本との違いは、統計量を計算するときに、経験分布と検定対象の累積分布関数の差分の上限(sup)を取るのではなく、その二つの標本それぞれの経験分布に対して、差分の上限の上限(sup)を取るというだけです。KS検定について調べるような人でこの説明でわからないという人もいないと思うので、数式等は省略します。(前回の記事を参照してください。)
便利な特徴としては、2標本のそれぞれのサイズは等しくなくても使える点ですね。
ただ、色々試した結果、それなりにサンプルサイズが大きくないとあまり使い物にならなさそうです。
この記事では、Pythonで実際に検定をやってみます。
前回のt分布からの標本と正規分布は、標準偏差が違うとはいえ流石に似すぎだったので、今回はちょっと変えて、カイ2乗分布と、正規分布を使います。
カイ2乗分布の自由度は4とし、すると期待値4、分散8になるので、正規分布の方もそれに揃えます。期待値や分散が違うならt検定やF検定で十分ですからね。
とりあえず分布関数を作り、可視化して見比べておきます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ks_2samp
from scipy.stats import norm
from scipy.stats import chi2
chi2_frozen = chi2.freeze(df=4) # 自由度4のカイ2乗分布 (期待値4, 分散8)
norm_frozen = norm.freeze(loc=4, scale=8**0.5) # 正規分布 (期待値4, 分散8)
# 確率密度関数を可視化
xticks = np.linspace(-10, 20, 301)
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(1, 1, 1)
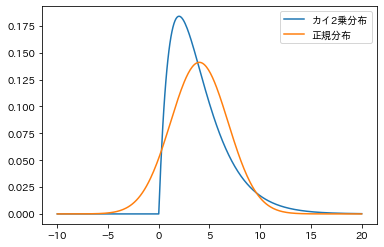
ax.plot(xticks, chi2_frozen.pdf(xticks), label="カイ2乗分布")
ax.plot(xticks, norm_frozen.pdf(xticks), label="正規分布")
ax.legend()
plt.show()出力はこちら。これはちゃんと検定で見分けて欲しいですね。
続いて、それぞれの分布から標本を取ります。サンプルサイズが違っても使える手法なので、意図的にサンプルサイズ変えました。
# それぞれの分布から標本を生成
chi2_samples = chi2_frozen.rvs(size=200, random_state=0) # カイ2乗分布からの標本
norm_samples = norm_frozen.rvs(size=150, random_state=0) # 正規分布からの標本さて、これでデータが取れたので、2標本KS検定やっていきます。
非常に簡単で、ks_2samp ってメソッドに渡すだけです。
ドキュメント: scipy.stats.ks_2samp — SciPy v1.9.0 Manual
例によって、alternative 引数で両側検定/片側検定などを指定できますが、今回両側でやるので何も指定せずにデフォルトのまま使います。
帰無仮説は「二つの標本が従う確率分布は等しい」です。有意水準は0.05とします。
結果がこちら。
print(ks_2samp(chi2_samples, norm_samples))
# KstestResult(statistic=0.17, pvalue=0.012637307799274388)統計量とp値が表示されました。p値が0.05を下回りましたので、帰無仮説を棄却し、二つの標本が従う確率分布は異なっていると判断します。
サンプルサイズさえそこそこ確保できれば、非常に手軽に使えて便利な手法だと思いました。
あとは個人的には、KS検定って5段階や10段階評価のような離散分布でも使えるのかどうか気になっています。まぁ、5段階の場合は単純にカイ2乗検定しても良いのですが、10段階以上になってくると自由度が高くてカイ2乗検定があまり使いやすくないので。何か情報がないか追加で探したり、自分でシミュレーションしたりしてこの辺をもう少し調べようと思います。