以前も紹介した、SciPyのカーネル密度推定のメソッド、gaussian_kdeの話です。
参考: SciPyによるカーネル密度推定
最近、多次元(と言っても2次元のデータですが)に対して、カーネル密度推定を行いたいことがあり、
どうせ1次元の場合と同じように使えるのだろうと適当に書いたら思うような動きにならず苦戦しました。
何をやろうとしたかというと、
[[x0, y0], [x1, y1], [x2, y2], …, [xn, yn]]
みたいなデータをそのままgaussian_kdeに渡してしまっていました。
ドキュメント: scipy.stats.gaussian_kde
をよく読むと、
Datapoints to estimate from. In case of univariate data this is a 1-D array, otherwise a 2-D array with shape (# of dims, # of data).
と書いてあります。
僕が渡そうとしたデータは shapeが[データ件数, 2(=次元数)]になっていたのですが、実際は
[2(=次元数), データ件数]の型で渡さないといけなかったわけです。
丁寧なことに、Examplesに取り上げられている例も1Dではなく2Dの例で、np.vstackとか使って書かれているので、以前の記事を書いた時にもっとしっかり読んでおけばよかったです。
使い方がわかったので、2次元のデータに対してやってみます。
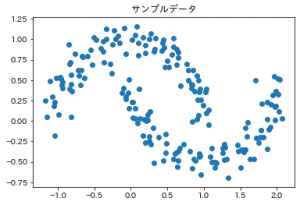
サンプルデータは今回はscikit-learnのmake_moonsを使いました。
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
# データ生成。 今回はラベルは不要なのでデータだけ取得する。
data, _ = make_moons(
n_samples=200,
noise=0.1,
random_state=0
)
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111, title="サンプルデータ")
ax.scatter(data[:, 0], data[:, 1])
plt.show()
サンプルデータはこんな感じです。
生成したデータを、gaussian_kdeにそのまま渡すとうまくいきません。
出来上がるモデルは、200次元のデータ2個を学習したものになっているからです。
from scipy.stats import gaussian_kde
# これはエラーは出ないが誤り
kde = gaussian_kde(data)
# 密度推定した結果を得ようとするとエラーになる。
print(kde.pdf([0, 0]))
# ValueError: points have dimension 1, dataset has dimension 200
きちんと、2次元のデータ200個を学習させるには、データを転置させて渡します。
from scipy.stats import gaussian_kde
# (データを、(次元数, データ件数) の型で渡す)
kde = gaussian_kde(X.T)
kde.evaluate を使って、推定した結果の値を得る時も、(次元数, データ件数)の形で、データを渡す必要があります。
(一点のみなら長さが次元数分の配列を渡せば良いです。)
# 点(1, 1)での値
print(kde.evaluate([1, 1]))
# [0.03921808]
# 4点(-0.5, 0), (0, 1), (0.5, 1), (1, 0) での値
print(kde.evaluate([[-0.5, 0, 0.5, 1], [0, 1, 1, 0]]))
# [0.07139624 0.2690079 0.2134083 0.16500181]
等高線を引いて図示する場合は次のように行います。(公式ドキュメントでは等高線ではなく、imshowで可視化していますね。)
こちらの記事も参考にしてください。
参考: matplotlibで等高線
# 等高線を引く領域のx座標とy座標のリストを用意する
x = np.linspace(-1.5, 2.5, 41)
y = np.linspace(-0.8, 1.3, 22)
# メッシュに変換
xx, yy = np.meshgrid(x, y)
# kdeが受け取れる形に整形
meshdata = np.vstack([xx.ravel(), yy.ravel()])
# 高さのデータ計算
z = kde.evaluate(meshdata)
# 可視化
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111, title="カーネル密度推定")
ax.scatter(data[:, 0], data[:, 1], c="b")
ax.contourf(xx, yy, z.reshape(len(y), len(x)), cmap="Blues", alpha=0.5)
plt.show()
結果がこちらです。
最後に、xもしくはy座標を固定して、断面をみる方法を紹介しておきます。
これはシンプルに、固定したい方は定数値でもう一方のデータと同じ長さの配列を作って、
固定しない方のデータを動かしてプロットするだけです。
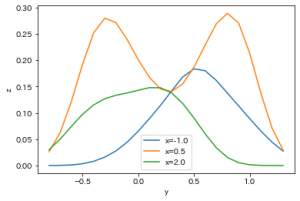
x=-1.0, 0.5, 2.0 の3つの直線で切ってみた断面を可視化すると次のようなコードになります。
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
for x_ in [-1.0, 0.5, 2.0]:
ax.plot(y, kde.pdf([[x_]*len(y), y]), label=f"x={x_}")
ax.set_ylabel("z")
ax.set_xlabel("y")
ax.legend()
plt.show()
結果がこちら。
だいぶ使い方の感覚が掴めてきました。