t-sne | 分析ノート

特に意図はないのですが、これまで高次元のデータを次元削減して可視化する時はPCAをよく使っていました。
基本的には線形変換なので、非線形な構造を持ってるデータはうまく特徴を捉えられません。
(それはそれで確認する意味があると思いますが。)

最近は、t-SNEという手法を使っている人が多いようなので、やってみたメモです。
irisだとPCAで十分うまく次元削減できてしまうので、今回はdigitsを使います(8*8の手書き数字画像データ)

t-SNE自体の実装は、scikit-leearnを使います。
ドキュメントはここ。


# ライブラリインポート
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

# データ準備
digits = load_digits()
X = digits.data
y = digits.target

# t-SNEの実行
tsne = TSNE(n_components=2)
X_tsne = tsne.fit_transform(X)

# 可視化
x_max, x_min = X_tsne[:, 0].max() * 1.05, X_tsne[:, 0].min() * 1.05
y_max, y_min = X_tsne[:, 1].max() * 1.05, X_tsne[:, 1].min() * 1.05
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(1, 1, 1, xlim=(x_min, x_max), ylim=(y_min, y_max))
ax.set_title("t-SNE")
for i, target in enumerate(y):
    ax.text(X_tsne[i, 0], X_tsne[i, 1], target)
plt.show()

これを実行して表示される画像がこちらです。

一部、変なところに分類されている数字があったり、1が複数のグループに分かれていたりするところはありますが、
非常に見事に分類できています。
これを好んで使う人がいるのも納得です。
高次元のデータの可視化のツールとして提唱されているだけはあります。

ちなみに、PCAで2次元に圧縮したのがこれ。

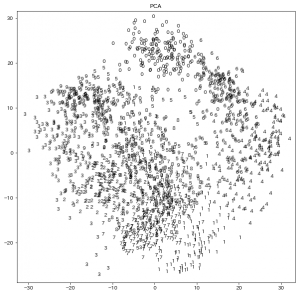
t-SNEと全く違う結果になっていますね。
(だからといって、PCAという手法自体が劣るというわけではないので注意です。)

タグ: t-sne

t-SNEでDigitsを次元圧縮して可視化してみた