ユール・ウォーカー方程式から求めた自己相関をサンプルから計算した自己相関と比較する

前回の記事で定常AR過程の自己相関係数を解析的に算出しました。
また、さらに以前の記事で、同じAR(3)過程に従う系列をpythonで生成しています。
このAR(3)過程のサンプルから、自己相関係数を計算したら、それは本当にユール・ウォーカー方程式から求めた値と一致するのかなというのが今回のテーマです。
結論を先に言っておくと非常に長い系列サンプルを用意しないと無理です。

では早速やってみましょう。
今回もサンプルはこれ。(適当に作った系列ですが、このブログでは高頻度で登場します。)

$$
y_t=1+\frac{11}{15}y_{t-1}-\frac{1}{3}y_{t-2}+\frac{1}{15}y_{t-3}+\varepsilon_t , \varepsilon_t \sim iid N(0,\sigma^2)
$$
ユール・ウォーカー方程式から求まる自己相関$\rho_k$の最初の8項は次のようになります。
$$
\begin{eqnarray}
\rho_0 &=& 1.0 \\
\rho_1 &=& 0.5555555555555556 \\
\rho_2 &=& 0.1111111111111111 \\
\rho_3 &=& -0.037037037037037035 \\
\rho_4 &=& -0.027160493827160487 \\
\rho_5 &=& -0.0001646090534979357 \\
\rho_6 &=& 0.006463648834019207 \\
\rho_7 &=& 0.0029841792409693643
\end{eqnarray}
$$

あとは、早速乱数で{y_t}を生成して、pandasの関数で自己相関を算出し、
上の値と比べてみましょう。

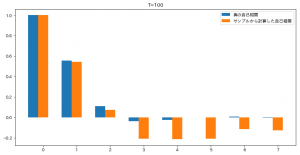
まず、100項算出してやってみたのが次のコードです。
注意点として、今回は系列の最初の方のデータを系列の期待値+撹乱項で生成しました。
また、撹乱項の標準偏差を$0.1$にしています。(つまり分散は$0.01$)。
これまで、$1$を使っていましたが、期待値が$1.875$の系列に対する撹乱項としてはちょっと分散が大きすぎましたので。

コードと出力はこちら。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

phi_1 = 11/15
phi_2 = -1/3
phi_3 = 1/15

# 過程の期待値
Ey = 1/(1-phi_1-phi_2-phi_3)

# 項数
T = 100

# 過程の生成
y = np.zeros(T)
# 初期値 (過程の期待値+乱数)
y[0] = Ey + np.random.normal(loc=0, scale=0.1)
y[1] = Ey + np.random.normal(loc=0, scale=0.1)
y[2] = Ey + np.random.normal(loc=0, scale=0.1)
for i in range(3, T):
    y[i] = 1 + phi_1*y[i-1] + phi_2*y[i-2] + phi_3*y[i-3] +\
                np.random.normal(loc=0, scale=0.1)

# 自己相関の算出
series = pd.Series(y)
series_autocorr = [series.autocorr(i) for i in range(8)]


# rho_values に、前回の記事で算出した自己相関が代入されている想定
# 可視化
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1, title='T=100')
ax.bar(np.arange(len(rho_values))-0.3, rho_values,  width=0.3, label='真の自己相関')
ax.bar(range(len(series_autocorr)), series_autocorr, width=0.3, label='サンプルから計算した自己相関')
ax.legend()
plt.show()

ラグが３以上になると全然ダメですね。

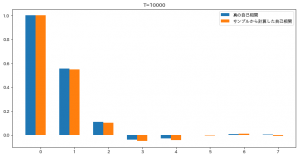
Tの値を 1000,10000 と増やして順に実行したのがこちらです。

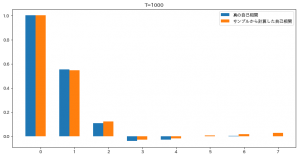
徐々に近づいてきたようにみます。

自己相関はpandasで結構手軽に計算できるので、
過去にも、時系列データをみたらとりあえず計算して眺めたりしていたのですが、
データ数がかなり大きくないとなかなか真の値に近いものにならないことがわかりました。
そもそも現実データには大量のノイズが入るので、ほんの数年分の
月次データ6ヶ月ラグとかみてもほとんどあてにならなさそうですね。