月: 2019年8月

前回の記事がNetworkXの頂点の書式についての記事だったので今回は辺の書式です。

ドキュメントは同じ場所です。
ドキュメント: draw_networkx

有向グラフの場合は矢印の形などもう少し項目が多いのですが、
無向グラフの場合は、太さと色とスタイル(単線、破線、ドットなど)が設定項目になります。

このうち、太さ(width) と 色(edge_color) は単一の値だけではなく、
辺の数と同じ長さの配列で指定することができます。

配列で指定した値は、 G.edge で取得できる辺の一覧の順番と対応するように設定されます。
(初めてNetworkXをいじった時はこの辺りをしらず、思った設定ができずにいました。)

細かいですがドキュメントにデフォルトの色は’r’ (赤)と書いてありますが、これはおそらくドキュメントの誤りです。
(何も指定しないと黒になります。)

edge_color (color string, or array of floats (default=’r’))

styleに指定できるのは次の4種類です。(スタイルの指定は辺別ではなく、全体で一つ指定する必要があります。)
solid|dashed|dotted|dashdot

それでは適当なグラフで実行してみましょう。

import networkx as nx
import matplotlib.pyplot as plt

# グラフを生成
G = nx.Graph()
G.add_cycle(range(5))

# 辺の順番を確認
print(G.edges)
# [(0, 1), (0, 4), (1, 2), (2, 3), (3, 4)]

# 可視化
nx.draw_networkx(
    G,
    edge_color=["r", "g", "m", "c", "y"],
    width=[1, 2, 3, 4, 5],
    style= "dashdot",
)
plt.show()

出力がこちら。

0と1を結んでるのが一番細い赤い線で、次に0と4を結んでるが緑の線で、
と G.edges の値と対応して設定が反映されました。

NetworkXのグラフを可視化するときに、もっと見た目を変えたいなと思うことは多々あると思います。
そのようなニーズに応えるために頂点と辺のそれぞれにいくつかのオプションが用意されています。
今回はその中から、頂点の書式に関するものをいくつか紹介します。

ドキュメント: draw_networkx

このページの node_xxx の形式で定義されているパラメーターがそれです。
この中から、node_size、node_color、node_shapeを使って、頂点の色や大きさを変えてプロットしてみましょう。
なお、node_shapeはグラフに対して1つですが、node_sizeとnode_colorは頂点ごとに設定を変えることができます。
ついでに font_family も設定して日本語のフォントを表示してみましょう。

# グラフの生成
G = nx.Graph()
for n in "あいうえお":
    G.add_node(n)

# 頂点の順番の確認。(node_size や node_color はこの順番で指定する)
print(G.nodes)
# ['あ', 'い', 'う', 'え', 'お']

nx.draw_networkx(
    G,
    node_shape="s",
    node_size=[100, 200, 300, 400, 500],
    node_color=["r", "g", "m", "c", "y"],
    font_family="IPAexGothic"
)
plt.show()

出力がこちら。

node_size はデフォルトが 300であることに注意しましよう。
node_shape には ‘so^>v<dph8’ のいずれかの文字が指定できます。

前の記事の続きです。
参考:NetworkXのグラフを可視化するときに頂点の座標を指定する
こちらの記事では、頂点を円形に並べるとき、三角関数を使って座標を指定しました。
それは自分の理解のためにやったのですが、実用上はあらかじめ用意さているレイアウト用の関数を使った方が楽です。

ドキュメント:Graph Layout
たとえば、
circular_layout
を使えば、円上にノードを配置できます。

次のコードのように使います。
グラフの構成と可視化結果は前回の記事と同じなので省略します。

pos = nx.circular_layout(G)
nx.draw_networkx(G, pos=pos, node_color="c")
plt.show()

久々のNetworkXの記事です。
今回はグラフを可視化するときに、明示的に頂点の座標を指定する方法を紹介します。

ドキュメントの Docs » Reference » Drawing
のページを見ると、draw_networkxなどの可視化関数がposという引数を受け取ることがわかります。
ここに、{頂点:(x座標, y座標), …} という形式の辞書を渡してあげると、可視化するときにその座標にノードを配置できます。
これを使って頂点を格子点においたり、一直線に並べたりできます。

いい感じに座標の辞書を作ってくれる関数もいくつか用意されているのですが、
今回は自分で直接円周上のてんを定義してやってみます。

まず一つ目の例は座標は指定せずにそのまま可視化したものです。

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np

# 12個の頂点と、ランダムに引いた辺を持つグラフを定義
node_labels = "abcdefghijkl"
G = nx.Graph()
G.add_nodes_from(node_labels)
for i in range(len(G.nodes)):
    for j in range(i+1, len(G.nodes)):
        if np.random.uniform() < 0.3:
            G.add_edge(node_labels[i], node_labels[j])

# 座標を指定せずに描写する
nx.draw_networkx(G, node_color="c")
plt.show()

結果がこちら。頂点はある程度バラバラに配置されていますね。

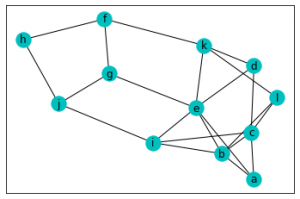
次にグラフはそのままで座標を指定してみます。

# 各頂点に対して円周上の座標を割り当てる
pos = {
        n: (np.cos(2*i*np.pi/12), np.sin(2*i*np.pi/12))
        for i, n in enumerate(G.nodes)
    }
print(pos)
'''
{'a': (1.0, 0.0),
 'b': (0.8660254037844387, 0.49999999999999994),
 'c': (0.5000000000000001, 0.8660254037844386),
 'd': (6.123233995736766e-17, 1.0),
 'e': (-0.4999999999999998, 0.8660254037844388),
 'f': (-0.8660254037844387, 0.49999999999999994),
 'g': (-1.0, 1.2246467991473532e-16),
 'h': (-0.8660254037844388, -0.4999999999999998),
 'i': (-0.5000000000000004, -0.8660254037844384),
 'j': (-1.8369701987210297e-16, -1.0),
 'k': (0.5, -0.8660254037844386),
 'l': (0.8660254037844384, -0.5000000000000004)}
'''

# 指定した座標を用いてグラフを可視化する
nx.draw_networkx(G, pos=pos, node_color="c")
plt.show()

結果がこちらです。

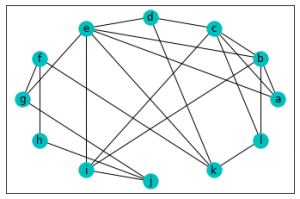
きちんと円周上に頂点が並びました。