標本平均と不偏分散の独立性の実験

最近数式ばかり増えてプログラムが登場してないのでちょっとした検証をやろうと思います。
今回行うのは、タイトルにある通り、標本平均と不偏分散の独立性です。

少し前の母平均の区間推定のところで、
$\sqrt{n}(\bar X-\mu)/s$は、自由度$n-1$の$t$分布に従う、とさらっと書きましたが、
これの前提になっているのが、
$\frac{\bar X -\mu}{\sigma/\sqrt{n}}$が標準正規分布に従うことと、
$\frac{(n-1)s^2}{\sigma^2}$が自由度$n-1$のカイ二乗分布に従うこと、
そして、この二つが独立であることです。
スチューデントの$t$分布の定義も参照。

この二つの値が独立であることって結構不思議な現象だと感じないでしょうか。
同じ標本から算出している値なので何か関係があっても良さそうです。

数式的に計算していって確かめることも可能なのですが、今回は乱数でいっぱい標本をとって、
プロットすることで確かに独立してるっぽいことを眺めて見たいと思います。

標本は$N(7, 2^2)$からとりました。サンプルサイズ$30$で、$500$回標本を取り、
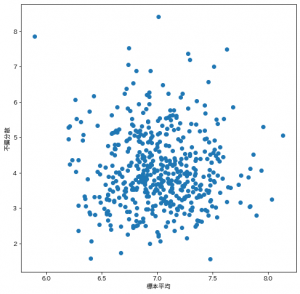
標本平均と不偏分散の相関係数を算出し、散布図にプロットしています。

コードと結果がこちら。

import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm

mu = 7
sigma = 2
sample_size = 30
sample_count = 500

result_list = []
for i in range(sample_count):
    X = norm(loc=mu, scale=sigma).rvs(sample_size)
    mu_ = X.mean()
    var_ = X.var(ddof=1)
    result_list.append({"mu_":  mu_, "var_": var_})

result_df = pd.DataFrame(result_list)
print("相関係数:"+str(np.corrcoef(result_df.mu_, result_df.var_)[0, 1].round(3)))
# 相関係数:-0.021

fig = plt.figure(figsize=(8, 8), facecolor="w")
ax = fig.add_subplot(111)
ax.set_xlabel("標本平均")
ax.set_ylabel("不偏分散")
ax.scatter(result_df.mu_, result_df.var_)
plt.show()

出力された散布図がこちらです。

相関係数は確かに0に近いですし、散布図もいかにも無相関っぽい形になりました。

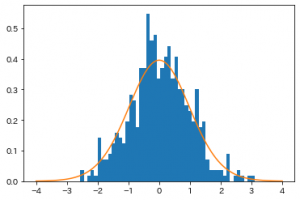
せっかくなので、各標本ごとに$t$値も算出して、$t$分布と見比べておきましょう。

import numpy as np
from scipy.stats import t

result_df["t_"] = np.sqrt(sample_size-1)*(result_df.mu_ - mu) / result_df.var_**0.5
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(result_df["t_"].values, bins=50, density=True)
ax.plot(np.linspace(-4, 4, 101), t(sample_size-1).pdf(np.linspace(-4, 4, 101)))
plt.show()

出力がこちら。

だいたいフィットしてそうですね。