カテゴリー: グラフ理論

以前紹介したpyvisの話です。
参考: pyvisでネットワーク可視化

最近久しぶりに使ったのですが、その時はそこそこ長いテキストをノードし、類似度によってエッジを貼るようなグラフを構築し可視化しました。

ノードに全文表示すると長すぎて視認性が全くなくなったので、ラベルにテキストのidや序盤の数文字を表示させていて、全文は別の場所で参照する、とやっていたのですがこれが非常に不便でした。

そこで、何かしら対応策ないかなと思っていたのですが、マウスオーバーした際にポップアップで表示するテキストを別途設定できることがわかりました。

設定自体も非常に簡単で、title という属性を指定するだけでした。

参考: Documentation — pyvis 0.1.3.1 documentation

これはノードだけでなくエッジに対しても設定できます。やってみましょう。

from pyvis.network import Network


# ネットワークのインスタンス生成
network = Network(
    notebook=True,  # これをTrueにしておくとjupyter上で結果が見れる
    cdn_resources='in_line',
    bgcolor='#ffffff',  # 背景色。デフォルト "#ffffff"
)

network.add_node(n_id=1, label="ラベル1", shape="box", title="ポップアップさせたいテキスト1")
network.add_node(n_id=2, label="ラベル2", shape="circle", title="ポップアップさせたいテキスト2")
network.add_edge(1, 2, label="辺のラベル", title="辺のポップアップ")

network.show("pyvis_sample1.html")

これで作成されたネットワーク図は、ノードやエッジにマウスオーバーした際にポップアップが表示されます。

簡単で便利ですね。

久々にNetworkXを使ったのですが、その時使った関数のメモです。

とあるノードの集合に対して、ある条件を満たすペアに対してエッジを張って行き、その結果出来上がった非連結なグラフから連結成分たちを取り出すという操作をやりました。

使った関数をこのブログでまだ紹介していなかったのでその周辺の操作も含めて紹介します。

とりあえず、サンプルのグラフを準備しておきましょう。連結成分が3組と、孤立ノードが2個ある次のようなグラフを作りました。

import networkx as nx


G = nx.Graph()
G.add_edges_from([
    (1, 2), (2, 3), (3, 1),  # コンポーネント1
    (4, 5), (5, 6),  # コンポーネント2
    (7, 8),  # コンポーネント3
])
G.add_nodes_from([9, 10])  # 孤立ノードを2個追加

見ての通り、(孤立してるのも含めて)連結成分が5組ありますね。

ここから連結している成分を取り出すには、nx.connected_components() というメソッドを使います。
参考: connected_components — NetworkX 3.4.2 documentation

結果がイテレーターで帰ってくるのですが今回の例は小さいのでlistにしておきましょう。

connected_components = list(nx.connected_components(G))
print(connected_components)
"""
[{1, 2, 3}, {4, 5, 6}, {8, 7}, {9}, {10}]
"""

はい、5組がそれぞれ出てきました。

孤立成分を除きたい場合は、この中からノードが2個以上あるものに絞り込むと良いでしょう。

print([c for c in connected_components if len(c) > 1])
# [{1, 2, 3}, {4, 5, 6}, {8, 7}]

逆に、ノードが1個のものに絞ると孤立成分が抽出できます。しかし、孤立成分を探す場合は、nx.isolates() という専用メソッドもあります。
参考: isolates — NetworkX 3.4.2 documentation

print(list(nx.isolates(G)))
# [9, 10]

また、連結成分の数や孤立成分の数を返す関数として、number_connected_components, number_of_isolates がそれぞれ用意されています。

print(nx.number_connected_components(G))
# 5
print(nx.number_of_isolates(G))
# 2

最後に、このノードが含まれてる連結成分が欲しいんだ、というケースもあると思います。その場合は、node_connected_component()を使います。
参考: node_connected_component — NetworkX 3.4.2 documentation

print(nx.node_connected_component(G, 4))
# {4, 5, 6}

帰ってきているのはそのノードを含む連結成分のノードの一覧(set)であって、サブグラフオブジェクトではないのでその点は注意してください。これは先ほどの連結成分の一覧を返してきてたメソッドと同様です。

pyvisはグラフを手軽に可視化できますし、pyvis自体のメソッドでノードやエッジを追加してグラフを構築することもできるので基本的な処理はこれだけで完結させることももちろんできます。しかし、グラフデータの分析をしていると、各種アルゴリズムが充実しているNetworkXでいろんな分析を行って、それを最後にpyvisで可視化したい、ということはよくある話です。

こういう場合、pyvisのネットワークオブジェクトが持っている、from_nxってメソッドが使えます。
参考: Documentation — pyvis 0.1.3.1 documentation

この記事の主題は「from_nxが便利だよ」で終わりなのですが、それだけではあんまりなので細かい話をいろいろ書いていきます。

まず、基本的な使い方ですが、from_nxは pyvisモジュールから直接呼び出せるメソッドではなく、pyvisのpyvis.network.Network オブジェクトに実装されているメソッドなので、まずそのインスタンスを生成します。以前の記事でも書いていますが、可視化するときのキャンパスサイズとか背景色などを指定して生成するやつですね。

具体的に適当なネットワークでやってみると次の様になります。

import networkx as nx
from pyvis.network import Network


# サンプルとして、NetworkXのグラフを生成
nx_graph = nx.Graph()
nx_graph.add_node("a")
nx_graph.add_node("b")
nx_graph.add_node("c")
nx_graph.add_edge("a", "b")
nx_graph.add_edge("b", "c")
nx_graph.add_edge("c", "a")


# ネットワークのインスタンス生成
network = Network(
    height="500px",
    width="500px",
    notebook=True,
    bgcolor='#ffffff',
    directed=False, 
)

# pyvisのネットワークに、NetworkXのグラフのノードやエッジ情報を取り込む。
network.from_nx(nx_graph)
# 可視化
network.show("sample.html")

結果は省略しますが、これで、a,b,cの3個のノードを持ったネットワークが可視化されます。

NetworkXで設定されていなかったがpyvisで可視化するときに必要な種類の情報はデフォルト値で補完されています。

# NetworkXのノードの情報
print(dict(nx_graph.nodes))
# {'a': {'size': 10}, 'b': {'size': 10}, 'c': {'size': 10}}

# pyvisに取り込んだときに、colorやshape、sizeのデフォルト値が設定されている。
print(network.nodes)
"""
[{'color': '#97c2fc', 'size': 10, 'id': 'a', 'label': 'a', 'shape': 'dot'},
 {'color': '#97c2fc', 'size': 10, 'id': 'b', 'label': 'b', 'shape': 'dot'},
 {'color': '#97c2fc', 'size': 10, 'id': 'c', 'label': 'c', 'shape': 'dot'}]
"""

# NetworkXのエッジの情報
print(dict(nx_graph.edges))
# {('a', 'b'): {'width': 1}, ('a', 'c'): {'width': 1}, ('b', 'c'): {'width': 1}}

# エッジはほぼそのまま取り込まれている。
print(network.edges)
# [{'width': 1, 'from': 'a', 'to': 'b'}, {'width': 1, 'from': 'a', 'to': 'c'}, {'width': 1, 'from': 'b', 'to': 'c'}]

ノードのサイズやエッジの太さは、デフォルト値をそれぞれ、default_node_size, default_edge_weight という引数で指定することもできるので、有効に使っていきましょう。例えばWebサイトのページ遷移データのネットワーク等で、NetworkX時点ではPVなどの大きい値をsizeとして計算していたら、それを可視化時のサイズとして使ってしまうとえらいことになります。

また、node_size_transf , edge_weight_transf という引数で、関数を渡しておくことで、それぞれの値を変換することもできます。元々の値が非常に大きい、または小さい場合にこれを使って補正することができますね。
例えば、
node_size_transf = (lambda x: x/10) とすると、ノードのサイズを1/10にできます。

ここで注意というか、version 3.2時点の pyvisにはバグがあって、エッジを持たない孤立ノードには node_size_transf が適用されません。

該当部分のソースコードがこちらです。

        if len(edges) > 0:
            for e in edges:
                if 'size' not in nodes[e[0]].keys():
                    nodes[e[0]]['size']=default_node_size
                nodes[e[0]]['size']=int(node_size_transf(nodes[e[0]]['size']))
                if 'size' not in nodes[e[1]].keys():
                    nodes[e[1]]['size']=default_node_size
                nodes[e[1]]['size']=int(node_size_transf(nodes[e[1]]['size']))
                self.add_node(e[0], **nodes[e[0]])
                self.add_node(e[1], **nodes[e[1]])

                # if user does not pass a 'weight' argument
                if "value" not in e[2] or "width" not in e[2]:
                    if edge_scaling:
                        width_type = 'value'
                    else:
                        width_type = 'width'
                    if "weight" not in e[2].keys():
                        e[2]["weight"] = default_edge_weight
                    e[2][width_type] = edge_weight_transf(e[2]["weight"])
                    # replace provided weight value and pass to 'value' or 'width'
                    e[2][width_type] = e[2].pop("weight")
                self.add_edge(e[0], e[1], **e[2])

        for node in nx.isolates(nx_graph):
            if 'size' not in nodes[node].keys():
                nodes[node]['size'] = default_node_size
            self.add_node(node, **nodes[node])

エッジが存在するノードの情報を取り込むときは、node_size_transfしてるのに、その後の孤立ノードの取り込みでは元のsizeとデフォルトノードサイズしか考慮してませんね。

これは将来のバージョンで修正されると思うのですが、こういうバグもあるので、サイズを変換したい場合はnode_size_transfではなく、自分で元のデータを修正してform_nxに渡した方が良いでしょう。

さらに、便利な機能なのですがノードのサイズやエッジの太さ以外の属性については、一通り全部コピーしてくれます。これを使って、可視化するときに設定したい情報などをNetowrkXのグラフオブジェクトの時点で設定しておくことも可能です。これはもちろん、pyvisのネットワークに変換してから付与してももちろん大丈夫なのですが。

ただ、例えばノードのクラスタリング結果を可視化時の色に反映させたい等の、何かしらのアルゴリズムの結果を可視化に使いたい場合は、NetworkXの時点で設定する方がやりやすいことが多いです。ただ、可視化時点でしか必要のない情報をNetworkXのオブジェクトに付与していくことに抵抗がある人もいるかもしれないので好みの問題だと思います。

基本的な話なのですが、以下の様にして属性を付与していけます。ノードを1つ、赤い三角形にしてみたり、エッジの一つを黒く塗ってラベルつけたりしています。

# 事前にグラフにいろいろ属性を設定できる。
nx_graph.nodes["a"]["color"] = "red"
nx_graph.nodes["a"]["shape"] = "triangle"

nx_graph.edges[("b", "c")]["color"] = "black"
nx_graph.edges[("b", "c")]["label"] = "hogehoge"

# 以降の Networkオブジェクトを作って from_nxするところは同じ。

以上が from_nx の説明です。とても便利なのでぜひ使ってみてください。

逆に、pyvisのNetworkをNetworkXのグラフに変換するメソッドは無いのかな、とも思ったのですが、専用のものはなさそうですね。まぁ、それぞれのライブラリの用途を考えれば必要もなさそうですし、どうしてもやりたければノードとエッジの情報をそれぞれ取り出してNetworkXのグラフを構築すればいいだけの話なのでそんなに難しくもなさそうです。

諸事情ありグラフが平面グラフかどうか手軽に判定する方法が必要になったので、その方法を調べました。(正確には、僕が調べたかったのは平面的グラフかどうかですが。)

平面グラフの定義についてはWikipediaがわかりやすいです。
参考: 平面グラフ – Wikipedia

簡単にいうと、グラフを2次元の図に可視化したときに、辺が交差しない様に書いたものが平面グラフです。そして、グラフによっては描き方によって辺が交差したりしなかったりするのですが、平面グラフと同型なグラフを平面的グラフと呼びます。
どうにか頑張れば辺が交差しない様に頂点を配置できるグラフが平面的グラフ、どうやってもどこかで交差してしまうグラフが平面的で無いグラフ、と考えた方がわかりやすいでしょう。

これをどうやって判定しようかなと考えていたのですが、networkxに専用のメソッドが用意されていました。
– check_planarity
– is_planar

is_planar の方がシンプルで、NetworkXのグラフオブジェクトを渡すとそれが平面的だったかどうかでTrue/Falseを返してくれます。
check_planarity の方は、平面的だったかどうかの情報だけでなく、埋め込みの情報も取得できます。これは、ノードをどの様に配置したら平面的になるかを示すものです。

is_planar の方が結果がシンプルなので速度面で早いとか何かメリットあるのかなと思っていたのですが、NetworkXのソースコードを見ると、内部でcheck_planarityを呼び出して、一個目の戻り値だけを返すという作りだったのでそういうメリットはなさそうです。

とりあえず、結果がシンプルなis_planarの方を使ってみます。

import networkx as nx


# 頂点4個の完全グラフは平面的
K4 = nx.complete_graph(4)
print(nx.is_planar(K4))
# True

# 頂点5個の完全グラフは平面的では無い
K5 = nx.complete_graph(5)
print(nx.is_planar(K5))
# False

簡単ですね。

check_planarityの方を使う場合は、戻り値として判定結果と埋め込み情報が返ってくるので、それぞれ個別に受け取ります。

is_planar, P = nx.check_planarity(K4)

print(is_planar)
# True
print(P)
# PlanarEmbedding with 4 nodes and 12 edges
# これは、ノードをキーにして辞書の様にして使うと中身を見れる。
print(P[0])
# {1: {'cw': 3, 'ccw': 2}, 2: {'cw': 1, 'ccw': 3}, 3: {'cw': 2, 'ccw': 1}}
# 上記の結果で、ノード0に、1, 2, 3と繋がるエッジがあることがわかる。
print(P[0][1])
# {'cw': 3, 'ccw': 2}
# これは、ノード0に他のノードがどの様な順番で繋がっているかを示し、
# ノード1の時計回りの隣が3,反時計回りの隣が2であることを示す。

注意しないといけないのは、平面的グラフだからといって描写したら平面グラフで描かれるとは限らないという点です。というか、平面グラフで描かれる方が稀です。さっきの例で挙げた頂点4個の完全フラフでさえ、普通に力学モデルで配置したらエッジが交差します。

そのため、NetworkXでは平面グラフ描写用のメソッドも持っています。
参考: planar_layout — NetworkX 3.1 documentation

spring_layoutと比較してみましょう。なぜか、with_labels引数のデフォルト値が違うのでTrueつけないとノードのidを表示してくれません。

import matplotlib.pyplot as plt


fig = plt.figure(figsize=(12, 6), facecolor="w")
ax = fig.add_subplot(121, title="spring_layout")
ax.axis("off")
nx.draw_networkx(K4, ax=ax)

ax = fig.add_subplot(122, title="planar_layout")
nx.draw_planar(K4, ax=ax, with_labels=True)

出てくる図がこちら。

draw_planar を使わなくても、他のアルゴリズム同様にlayout系のメソッドで座標を取得してそれで描写することもできます。
参考: planar_layout — NetworkX 3.1 documentation

pos = nx.layout.planar_layout(K4)
print(pos)
"""
{0: array([-1.   , -0.375]),
 1: array([ 1.   , -0.375]),
 2: array([0.   , 0.125]),
 3: array([0.   , 0.625])}
"""

nx.draw_networkx(K4, pos=pos)
# 結果略

前回に引き続き、Louvain法の話です。前回はPythonで使う方法を紹介しましたが、今回はこの手法が利用しているモジュラリティ(modularity)という指標について検証していきます。そもそもなぜこの式でグラフのノードのクラスタを評価できるのかってのを確認しましょう。
(ちなみに、モジュラリティを最大化するアルゴリズムについては今回の記事では取り上げません。あくまでもモジュラリティの定義について見ていきます。)

前回の記事でも書いてるのですが今回の記事では主役なので定義式を再掲します。

$$Q=\frac{1}{2m}\sum_{ij}\left[A_{ij}\ -\ \frac{k_ik_j}{2m} \right]\delta(c_i, c_j).$$

$A_{ij}$: ノード$i$, ノード$j$間のエッジの重み。
$k_i, k_j$: ノード$i$, ノード$j$それぞれに接続されたエッジの重みの合計。
$m$: グラフの全てのエッジの重みの合計。
$c_i, c_j$: ノード$i$, ノード$j$それぞれが所属しているコミュニティ。
$\delta$: クロネッカーのデルタ。二つの引数が等しければ1でそれ以外は0を返す関数。

一見しただけだと、これでクラスタを評価できるってわかりにくいですよね。

順番に見ていきましょう。

まず、$\delta(c_i, c_j)$の部分です。これ、$c_i$と$c_j$が別のクラスタだったら値が$0$なので、$\sum$のそれらの項は消滅し、さらに同じクラスタだったら値が$1$になるので、それらの項はそのままの値で残ります。

なのでこの式はこうなります。

$$Q=\frac{1}{2m}\sum_{c_iとc_jが同じクラスタとなるi,j}\left[A_{ij}\ -\ \frac{k_ik_j}{2m} \right].$$

そして、$A_{ij}$はエッジの重みなので、和の中身の前半部分だけに着目すると、次の様に言えます。

$$\frac{1}{2m}\sum_{c_iとc_jが同じクラスタとなるi,j}A_{ij} = \frac{1}{2m}\{クラスタ内部のエッジの重みの総和\}$$

$m$はクラスタに関係なく、グラフによって定まってる定数なので無視して良いですから、この部分は確かに同じクラスタの中にたくさんエッジがあると値が大きくなり評価指標としての意味を持っている様に見えます。

ただし、この項しかないと、全部のノードを1個のクラスタとした場合に$Q$が最大となっしまうので、それに対応する必要があります。そこで登場するのが残りの項です。

もし、ノード$i$とノード$j$の間にエッジがなかったりあってもウェイトが非常に小さかったりすると、負の数を足すことによってモジュラリティが下がる様になってるのです。たとえば、エッジがない場合、$A_{ij}$が0ですから、$A_{ij}\ -\ \frac{k_ik_j}{2m} = -\frac{k_ik_j}{2m} $です。

そして、$k_i$、$k_j$はそれぞれのノードに接続されたエッジの重みの和ですから、重みの大きなエッジをたくさん持っているノード間についてはこの値の絶対値は大きくなります。

つまり、エッジがたくさんあるノード同士にも関わらずそれらのノード間にエッジがなかったら強くペナルティを課すよ、ってのがこの項の意味なのです。
分母の$2m$とかにもちゃんと意味があるのですが細かい話になるので割愛します。これらの細かい工夫により、-0.5から1の値を取る指標となっています。計算量とのバランスもとりながら非常によく考えられた指標だと思いました。

最後に、前回の記事でも少しだけ触れているのですが、この$\sum_{ij}$が取る和の$ij$部分について確認したのでその話書いておきます。

これは$i$と$j$がそれぞれ独立に全てのパターンを取ります。$(i, j)$と$(j, i)$は個別に足されるし、$(i, i)$も考慮されるってことですね。ライブラリの結果と、自分で実装した結果を並べてみて確認しました。とりあえず復習兼ねて前回のサンプルのグラフでやります。まずライブラリ利用。

import numpy as np
import networkx as nx
import community

# 前回の記事で生成したのと同じグラフを再現する。
# 30個のノード
node_list = list(range(30))

# 同じクラスタ内は0.5, 別クラスタは0.02の確率でエッジを生成する
edge_list = []
np.random.seed(1)  # シード固定
for i in range(30):
    for j in range(i+1, 30):
        if i // 10 == j // 10:
            if np.random.rand() < 0.5:
                edge_list.append((i, j))
        else:
            if np.random.rand() < 0.02:
                edge_list.append((i, j))

# グラフ生成
G = nx.Graph()
G.add_nodes_from(node_list)
G.add_edges_from(edge_list)

# コミュニティーの検出
partition = community.best_partition(G)

# ライブラリによるモジュラリティの計算
print(community.modularity(partition, G))
# 0.5316751700680272

同じ値を自分で計算して出してみましょう。エッジのウェイトが全部1なので、$m$はただのエッジの本数になるし、$k_i$, $k_j$はそれぞれのノードの次数に等しいことに注意してください。

Q = 0
m = G.size()
# iと jは全部の組み合わせをとる。
for i in range(len(G)):
    for j in range(len(G)):
        if partition[i] == partition[j]:
            # ノードi と ノードjの間にエッジがあったら1(ウェイト)を足す
            if (i, j) in G.edges:
                Q += 1 
            
            # Σの後半部分
            Q -= G.degree(i) * G.degree(j) / (2*m)
# 全体を2mで割る
Q/=2*m
print(Q)
# 0.5316751700680273

一致してますね。

ここから余談ですが、Qは -0.5から 1の値を取りますが、どんなグラフについてもQが-0.5を取ったり1を取ったりする分割が存在するわけではなさそうです。上記のサンプルでも0.53程度に留まっていますしね。

-0.5 の方は、完全２部グラフを構築して、さらにその2部をそれぞれコミュニティとすることで、同じクラスタ内部には1本もエッジがないのに別クラスタのノード間には必ずエッジが存在するという状態にすると発生します。

また、逆にQが大きくなるのは非連結な多数の完全グラフからなるグラフをそれぞれの完全グラフを一つのクラスタとすると、非連結なグラフが増えるにつれて1に近づいていくのを確認できています。ただ、近づくだけで1になることはないんじゃないでしょうか。(証明はできていませんが。)

便利なのでなんとなく使っていた手法でしたが、改めて指標を検証し複数のグラフや分割について自分で計算してみたことで理解を深めることができました。

モジュラリティは定義中に記号多いですしぱっと見難しそうに見えるのですが、落ち着いて見れば四則演算だけで構成されている非常にシンプルな指標なので、興味があれば皆さんもいろいろ試して遊んでみてください。

昔、グラフ関係の記事を書いてた頃に書いてたと思ってたら、まだ書いてなかったので、グラフのコミュニティーを検出する方法を書きます。

グラフのコミュニティ検出というのは、グラフのノードを複数のグループに分け、同じグループ内のノード同士ではエッジが密で、異なるグループのノード間ではエッジが疎になる様にすることを言います。人の集まりを仲良しグループでいくつかの組に分けるのに似ていますね。この記事の最後にも結果の例の画像をつけていますのでそれをみていただくとイメージがつきやすいと思います。

複数のアルゴリズムが存在するのですが、僕が一番気に入っていてよく使っているのはLouvain法による方法なのでこれを紹介していきます。
参考: Louvain method – Wikipedia

このLouvain法では、グラフとコミュニティに対してモジュラリティ(modularity)という指標を定義し、このモジュラリティが最大になる様なコミュニティの分け方を探すことでグラフのノードを分割します。モジュラリティの定義式はWikipediaにもありますが以下の通りです。

$$Q=\frac{1}{2m}\sum_{ij}\left[A_{ij}\ -\ \frac{k_ik_j}{2m} \right]\delta(c_i, c_j).$$

ここで、各記号の意味は以下の通りです。
$A_{ij}$: ノード$i$, ノード$j$間のエッジの重み。
$k_i, k_j$: ノード$i$, ノード$j$それぞれに接続されたエッジの重みの合計。
$m$: グラフの全てのエッジの重みの合計。
$c_i, c_j$: ノード$i$, ノード$j$それぞれが所属しているコミュニティ。
$\delta$: クロネッカーのデルタ。二つの引数が等しければ1でそれ以外は0を返す関数。

元論文を読めていないのですが、ライブラリの挙動を確認した結果によると、和の$ij$は$i$, $j$の全てのペアを渡る和で$i,j$の組み合わせとそれを入れ替えた$j, i$の組み合わせを両方取り、さらに$i=j$となる自己ループなエッジも考慮している様です。

さて、実際にやってみましょう。Pythonでは、communityというライブラリがあり、Louvain法が実装されています。(networkx自体にも他のコミュニティ検出のアルゴリズムが実装されているのですが、Louvain法は別ライブラリになっています。)

pipyでの登録名がpython-louvainなので、インストール時のコマンドが以下であることに注意してください。Pythonでimportするときと名前が違います。

$ pip install python-louvain

ドキュメントはこちら
参考: Community detection for NetworkX’s documentation — Community detection for NetworkX 2 documentation

早速使ってみましょう。例としてコミュニティがわかりやすいグラフを乱数で生成します。
0~29のノードを持ち、0~9, 10~19, 20〜29が同じコミュニティで、同コミュニティー内では50%の確率でエッジが貼られていて異なるミュにティだと2%の確率でしかエッジがないという設置です。

import numpy as np
import networkx as nx
import community

# 30個のノード
node_list = list(range(30))

# 同じクラスタ内は0.5, 別クラスタは0.02の確率でエッジを生成する
edge_list = []
np.random.seed(1)  # シード固定
for i in range(30):
    for j in range(i+1, 30):
        if i // 10 == j // 10:
            if np.random.rand() < 0.5:
                edge_list.append((i, j))
        else:
            if np.random.rand() < 0.02:
                edge_list.append((i, j))

# グラフ生成
G = nx.Graph()
G.add_nodes_from(node_list)
G.add_edges_from(edge_list)

さて、グラフができたのでコミュニティ検出をやっていきます。これものすごく簡単で、best_partitionというメソッドにnetworkxのグラフオブジェクトを渡すとノードと所属するグループの辞書として結果が帰ってきます。

注意点ですが、アルゴリズムの高速化のための工夫の弊害により絶対にベストな分割が得られるというわけではなく少々確率的な振る舞いをします。今回のサンプルコードでは非常にわかりやすい例を用意したので一発で成功していますが、通常の利用では何度か試して結果を比較してみるのが良いでしょう。

ではやっていきます。

partition = community.best_partition(G)

print(partition)
"""
{0: 2, 1: 2, 2: 2, 3: 2, 4: 2, 5: 2, 6: 2, 7: 2, 8: 2, 9: 2,
10: 0, 11: 0, 12: 0, 13: 0, 14: 0, 15: 0, 16: 0, 17: 0, 18: 0, 19: 0,
20: 1, 21: 1, 22: 1, 23: 1, 24: 1, 25: 1, 26: 1, 27: 1, 28: 1, 29: 1}
"""

0〜9は2で、10〜19は0で、20〜29は1と、綺麗に分類できてますね。

画像に表示してみましょう。ドキュメントのサンプルコードだとlist(partition.values())と辞書の値をそのまま可視化メソッドに渡していますが、辞書型のデータなので順序は保証されておらずこれはリスキーな気がします。実はそれでもうまくいくのですが念のため、ノードと順番が揃う様に配列として取り出してそれを使う様にしました。

# ノードの並びと同じ順でグループのリストを配列として取得する。
partition_list = [partition[n] for n in G.nodes]
# 配置決め
pos = nx.spring_layout(G, seed=3)
# 描写
nx.draw_networkx(G, node_color=partition_list, cmap="tab10", pos=pos)

結果がこちらです。

綺麗に3グループに分かれていますね。

ちなみに、このグループ分けのモジュラリティを取得するメソッドもあります。グループ分けとグラフ本体のデータをそれぞれ渡すことで使えます。

print(community.modularity(partition, G))
# 0.5316751700680272

結構高いですね。

このブログではネットワーク(グラフ)の可視化にはNetworkX(+Matplotlib)やGraphvizを使って来たのですが、最近pyvisというライブラリを気に入っていてよく使うようになりました。
訪問者の方にもぜひ触ってみていただきたいので軽く紹介していきます。

まず、どんなものが描けるのかの例です。このpyvisはvis.jsというJavaScriptのライブラリのPythonラッパーになっています。 そのため、vis.jsのドキュメントの examples ページを見るとさまざまな可視化例が載っています。こんなのが作れるんだ！ってモチベーションが上がるので一度見ていただけると幸いです。(実はこのvis.jsはネットワークの可視化以外の機能も持っているのですが、もっぱら僕の関心はネットワークの可視化にあります。)
参考: Vis Network Examples

各サンプルなのですが、それぞれのサンプル個別のページのアクセスして触っていただけると分かる通り、このライブラリで描いたネットワーク図はノードをマウスでドラッグして動かせます。これが1番のお勧めポイントです。また、単一のHTMLファイルで結果が出力されるので仕事で可視化した場合は結果は他の人に共有しやすいというのもいいですね。

それでは早速、使ってみましょう。pyvis 自体のドキュメントはこちらですが、母体のvis.jsのドキュメントや、Examplesのソースコードなども目を通されると理解が深まると思います。

本当に適当に作ってみました。インスタンス作って、ノードとエッジを追加して、最後HTML出力のメソッドを呼び出して完成です。

from pyvis.network import Network


# ネットワークのインスタンス生成
network = Network(
    height="300px",  # デフォルト "500px"
    width="400px",  # デフォルト "500px"
    notebook=True,  # これをTrueにしておくとjupyter上で結果が見れる
    bgcolor='#ffffff',  # 背景色。デフォルト "#ffffff"
    directed=True,  # Trueにすると有向グラフ。デフォルトはFalseで無向グラフ
)

# add_node でノードを追加
# label は省略可能。省略するとidと同じになる。
network.add_node(n_id=1, label=1, shape="circle")
network.add_node(n_id=2, label=2, shape="box", color="green")
network.add_node(n_id=3, label=3, shape="triangle")
network.add_node(n_id=4, label=4)  # shape を省略すると、 shape="dot"と同じになる

# add_edge でエッジを追加
network.add_edge(1, 2,)
network.add_edge(2, 4, width=2)  # width で太さを変えられる
network.add_edge(3, 4, smooth="dynamic")  # smooth を指定することで、エッジを曲線にできる
network.add_edge(4, 3, smooth="dynamic")  # エッジを曲線にすると双方向のエッジを別の線にできる。(直線だと重なる)

# 指定したファイル名でHTMLを出力。
network.show("pyvis_sample1.html")

出来上がりはこんな感じです。

動かせるっていいですね。

ソースコード中にコメントをいろいろ書いてますが、ノードもエッジも細かい設定がたくさんできます。pyvisのドキュメントだとこのページが該当するのですが、そこまで丁寧ではないので、vis.jsの方のドキュメントを読み込んで、そこから類推して使った方が理解が早いかもしれません。(場合によっては出力されたHTMLファイルを直接編集するとか。)
vis.js の方のドキュメントでは以下のページに設定可能な項目がまとまっています。
– vis.js – Nodes documentation.
– vis.js – Edges documentation.

もう一つ、HTML出力前に network.show_buttons() ってメソッドを実行しておくと、大量のコントロールボタンがHTMLに出力されます。(jupyterでは表示されないので、別途ブラウザでHTMLファイルを開いてください。)
これを使うと、ノードやエッジのオプションやノード配置の計算に使われている力学の設定などをインタラクティブに変更できます。

# ネットワークの作成までのコードは共通
network.show_buttons()  # 各種ボタンの表示
network.show("pyvis_sample2.html")

これも楽しいので試してみてください。(ただ、楽しいだけで今のところ有効な使い方を見出せずすみません。) ボタン多すぎ、って場合は、ドキュメントにある通り、filter_ って引数で絞り込めます。

最後に、vis.js から pyvis に移行した人への注意が一つあります。(僕はこのパターン。当初直接HTMLでvis.jsファイル書いてました。)
それは、 node の shape のデフォルト値で、 HTML/JavaScriptで書いてる場合、shapeを何も指定しなかった場合の挙動は”ellipse”です。しかし、pyvis は add_nodeでshape 引数を省略すると、出力されるJavaScirptに勝手に “shape”: “dot” をつけます。

何も指定せずに超単純なネットワークを描いたときの挙動が違うので僕は結構戸惑いました。
(ellipseは図の内側にラベルが入り、dotはラベルが外に出るという違いがちょっと気に入らなかった。その辺の話も、上記の Nodes documentation に書いてあります。)

“Python言語によるビジネスアナリティクス”と言う本の中に、NetworkXについての記述があるのですが、
その演習問題(問題43)として8-クイーン問題が出題されています。
面白そうだったので挑戦してみたところ、なんとか解けました。
この問題がネットワーク解析に関係あるとは意外ですね。

まず、8-クイーン問題については、Wikipediaの説明が分かりやすいと思います。
エイト・クイーン – Wikipedia

簡単に言うと、8×8の盤面状にチェスのクイーン(将棋の飛車と角を足した動きができる最強のコマ)をお互いに取り合えない位置に並べるパズルです。
正解は92通り(盤面の反転や回転を除いた本質的なものは12通り)あるそうです。

さて、これを解くために、次のアプローチを考えました。

1. 8×8の各マスをノードとするグラフを構築する。
2. クイーンがお互いに取り合えるマス同士をエッジで結ぶ。
3. そのグラフの補グラフを取得することで、クイーンがお互いに取り合えないマス通しが結ばれたグラフを作る。
4. ノード数が8のクリーク(その中に含まれる全てのノードが結ばれている部分グラフ)を探索する。

最初からお互いに取り合えないマスの間を結ぶのではなく、2.と3.に分けてるのはその方が実装がシンプルになるからです。

import networkx as nx

# 盤面の一辺のマス数
bord_size = 8

# グラフ生成
G = nx.Graph()

# ノードを作成する
for i in range(bord_size):
    for j in range(bord_size):
        G.add_node((i, j))

# 同じ行か同じ列に並ぶノードをエッジで結ぶ
for i in range(bord_size):
    for m in range(bord_size):
        for n in range(m+1, bord_size):
            G.add_edge((i, m), (i, n))
            G.add_edge((m, i), (n, i))

# 同じ斜め線状に並ぶノードをエッジで結ぶ
for n1 in G.nodes:
    for n2 in G.nodes:
        if n1 == n2:
            continue
        elif n1[0]+n1[1] == n2[0]+n2[1]:
            G.add_edge(n1, n2)
        elif n1[0]-n1[1] == n2[0]-n2[1]:
            G.add_edge(n1, n2)


# 補グラフを得る (お互いに取り合わない辺が結ばれている)
G_complement = nx.complement(G)

# サイズが変の数に等しいクリークの一覧を得る
answers = [
        clieque for clieque in nx.find_cliques(G_complement)
        if len(clieque) == bord_size
    ]

# 得られた解の個数
print(len(answers))
# 92

こうして、92個の解が得られました。
あとは実際にこれを可視化してみましょう。

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(12, 30), facecolor="w")

for i, answer in enumerate(answers, start=1):
    bord = np.zeros([bord_size, bord_size])
    ax = fig.add_subplot(16, 6, i)

    for cell in answer:
        bord[cell] = 1

    ax.imshow(bord, cmap="gray_r")

plt.show()

出力がこちらです。　一個一個みていくと確かに 縦横斜めにダブらない様にQueen(黒い点)が配置できています。
ただ、全部相異なることを確認するのは少し手間ですね。

もともと出題されていた本には解答が載っていないので、
もしかしたらこの記事のコードでは相当非効率なことをやっているかもしれませんが、
おそらくこんなイメージで解くのだと思います。

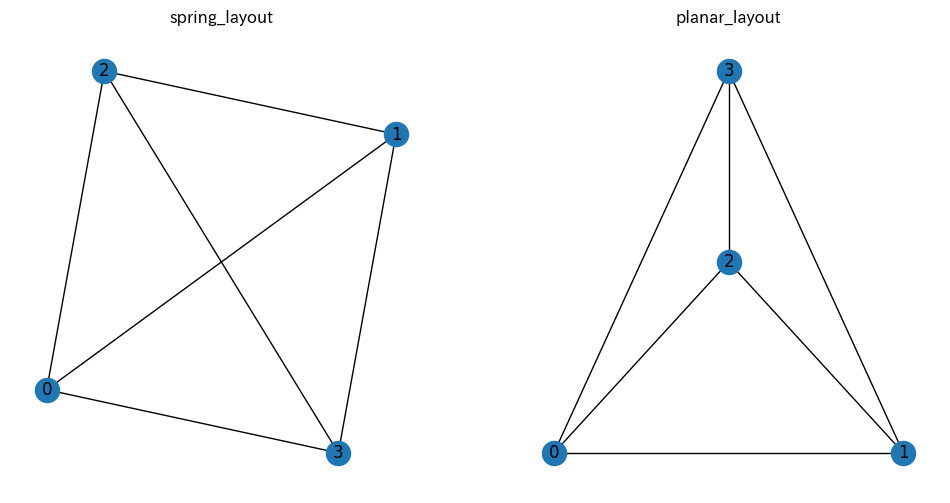
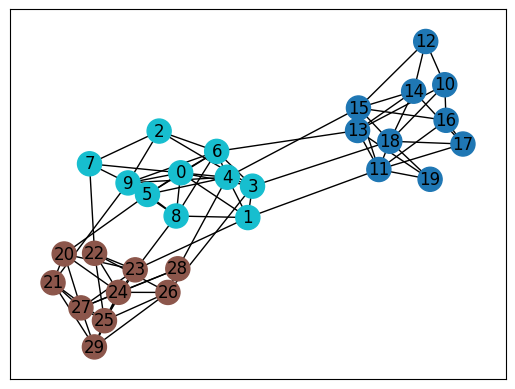
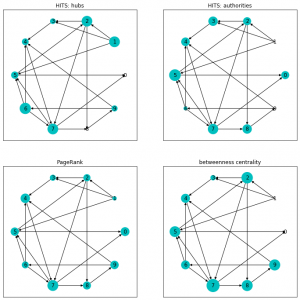
NetworkXでグラフを可視化する時、
２次元だとエッジが多すぎていわゆる毛玉状態になり、わけがわからないけど3次元だと少しマシになるということがあったので、3次元でプロットする方法を紹介しておきます。

公式ドキュメントの 3D Drawing のページを見ると、
Mayavi2 というのを使う方法が紹介されています。
ただ、僕がこれを使ったことがないのと、Matplotlibで十分できそうだったので、Matplotlibでやってみました。
Mayavi2 はこれはこれで便利そうですし、可視化の幅を広げられそうなので近いうちに試します。

まず、可視化するグラフデータを生成します。
今回はいつもみたいにランダム生成ではなく、エッジを具体的に指定して構築しました。
出来上がるのはサッカーボール型の多面体です。
(実はこのデータ生成の方が3次元プロットより苦労しました。)

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import networkx as nx
import numpy as np

# エッジデータを生成
edge_list = [
    (0, 1), (1, 2), (2, 3), (3, 4), (4, 0),
    (0, 5), (1, 6), (2, 7), (3, 8), (4, 9),
    (5, 10), (10, 11), (11, 6), (6, 12), (12, 13),
    (13, 7), (7, 14), (14, 15), (15, 8), (8, 16),
    (16, 17), (17, 9), (9, 18), (18, 19), (19, 5),
    (11, 20), (20, 21), (21, 12), (13, 22), (22, 23),
    (23, 14), (15, 24), (24, 25), (25, 16), (17, 26),
    (26, 27), (27, 18), (19, 28), (28, 29), (29, 10),
    (21, 30), (30, 31), (31, 22), (23, 32), (32, 33),
    (33, 24), (25, 34), (34, 35), (35, 26), (27, 36),
    (36, 37), (37, 28), (29, 38), (38, 39), (39, 20),
    (31, 40), (40, 41), (41, 32), (33, 42), (42, 43),
    (43, 34), (35, 44), (44, 45), (45, 36), (37, 46),
    (46, 47), (47, 38), (39, 48), (48, 49), (49, 30),
    (41, 50), (50, 42), (43, 51), (51, 44), (45, 52),
    (52, 46), (47, 53), (53, 48), (49, 54), (54, 40),
    (50, 55), (51, 56), (52, 57), (53, 58), (54, 59),
    (55, 56), (56, 57), (57, 58), (58, 59), (59, 55),
]

# 生成したエッジデータからグラフ作成
G = nx.Graph()
G.add_edges_from(edge_list)

さて、データができたので早速3次元空間にプロットしてみましょう。
方法は簡単で、以前紹介したmatplotlibの3次元プロットの方法で、
ノードとエッジを順番に出力するだけです。

ノードの方はこちらの記事が参考になります。
参考: matplotlibで3D散布図
エッジの方はまだ直接的に消化はしていませんが、2次元空間に直線を引く時と同様に、
ax.plot で描けます。

実際にやってみたのが以下のコードです。
比較用に２次元にプロットしたものを横に並べました。

# spring_layout アルゴリズムで、3次元の座標を生成する
pos = nx.spring_layout(G, dim=3)
# 辞書型から配列型に変換
pos_ary = np.array([pos[n] for n in G])

# ここから可視化
fig = plt.figure(figsize=(20, 10), facecolor="w")
ax = fig.add_subplot(121, projection="3d")

# 各ノードの位置に点を打つ
ax.scatter(
    pos_ary[:, 0],
    pos_ary[:, 1],
    pos_ary[:, 2],
    s=200,
)

# ノードにラベルを表示する
for n in G.nodes:
    ax.text(*pos[n], n)

# エッジの表示
for e in G.edges:
    node0_pos = pos[e[0]]
    node1_pos = pos[e[1]]
    xx = [node0_pos[0], node1_pos[0]]
    yy = [node0_pos[1], node1_pos[1]]
    zz = [node0_pos[2], node1_pos[2]]
    ax.plot(xx, yy, zz, c="#aaaaaa")
    
# 比較用 : 通常の２次元軸へのプロット
ax = fig.add_subplot(122)
nx.draw_networkx(G, edge_color="#aaaaaa")

# 出来上がった図を表示
plt.show()

このコードで以下の図が出力されました。

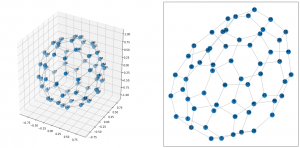
３次元の方がサッカーボール として綺麗な形になっているのがみて取れると思います。
座標軸の数値はいらないのでこれを消すなどの工夫を加えたらもっと良いかもしれませんね。

blog記事には静止画で貼り付けましたが、
jupyter notebook で実行する時は、
%matplotlib notebook を実行しておくと、
３次元プロットはグリグリ動かして確認ができます。
結構便利なので機会があれば試してみてください。

追記(2022/11/16) : エッジの描写についての解説

3次元にプロットするところの、エッジ(線)の描写部分について質問いただきましたので、解説します。

該当コードはここですね。

for e in G.edges:
    print(e)
    node0_pos = pos[e[0]]
    node1_pos = pos[e[1]]
    xx = [node0_pos[0], node1_pos[0]]
    yy = [node0_pos[1], node1_pos[1]]
    zz = [node0_pos[2], node1_pos[2]]
    ax.plot(xx, yy, zz, c="#aaaaaa")

まず、最初のfor文ですが、これはグラフのエッジをループさせています。変数eエッジの中の一つが格納され、それがどのノードからどのノードへのエッジなのかの情報がただのタプルとして入ってます。1個目だけprintしてみます。一番最初に作ったエッジデータの1個目ですね。

for e in G.edges:
    print(type(e))
    print(e)
    break #　　打ち切り
"""
<class 'tuple'>
(0, 1)
"""

エッジが(0, 1)ですから、まずノード0からノード1へ線をひこう、というのが以降の処理です。そのために、ノード0とノード1はどの座標に配置されているのかの情報が必要になります。

その座標が spring_layout ってアルゴリズムで推定して、ノード:座標の形でposって変数に辞書で入ってます。(上の方のコード参照)
中身を見ておきましょう。全ノード分含まれているのですが、最初の5件blogに載せます。

from pprint import pprint


pprint(pos)
"""
{0: array([-0.6114604 ,  0.62195763,  0.31867187]),
 1: array([-0.5150625 ,  0.74024425, -0.01842863]),
 2: array([-0.17471886,  0.96503904,  0.00644528]),
 3: array([-0.02757867,  0.98970947,  0.35055788]),
 4: array([-0.30497656,  0.77198962,  0.53307487]),
# 以下略
""" 

e = (0, 1) ですから、 e[0] = 0, e[1] = 1です。(最初のedgeはインデックスと中身が一致しててややこしく、すみません)
これを使って、エッジが繋いでる2頂点の座標を取得します。アルゴリズムが乱数使っているので具体的な値は実行するたびに変わりますのでご注意ください。

node0_pos = pos[e[0]]
node1_pos = pos[e[1]]

# 一つ目のノードの座標
print(node0_pos)
# [-0.6114604   0.62195763  0.31867187]

# 二つ目のノードの座標
print(node1_pos)
# [-0.5150625   0.74024425 -0.01842863]

具体的な座標が定まったので、この2点の間に線を引きます。これは、Axes3Dをimportした状態のmatplotlibのplotメソッドで実行します。

この時にax.plot(1点目の座標, 2点目の座標)と渡すと動かないのです。
2次元のplotにおいても ax.plot(x座標の一覧, y座標の一覧) とデータを渡すように、3次元plotでもax.plot(x座標の一覧, y座標の一覧, z座標の一覧)とデータを渡す必要があります。

xxとかyyとか変な変数名で恐縮ですが、それを続くコードでやってます。

# x座標, y座標, z座標をそれぞれ取り出し
xx = [node0_pos[0], node1_pos[0]]
yy = [node0_pos[1], node1_pos[1]]
zz = [node0_pos[2], node1_pos[2]]

# 中身確認
print(xx)
# [-0.6114604015979618, -0.5150625045997115]
print(yy)
# [0.6219576319265612, 0.740244253223188]
print(zz)
# [0.3186718713992598, -0.01842863446943393]

そして、出来上がったxx,yy,zz を ax.plot()に渡してエッジが1本引けたことになります。
c=”#aaaaaa” はただの色設定(灰色)なので問題ないと思います。

これで1つ引けるので、あとはfor文で各エッジを変数eに格納して順次繰り返しています。

HITSアルゴリズム(Hyperlink-Induced Topic Search)という手法がありますので紹介します。
NetworkXのドキュメントにおいて、PageRankと一緒に Link Analysis のページにあることから存在を知りました。
参考: NetworkXのドキュメントの Link Analysis
論文: A Survey of Eigenvector Methods for Web Information Retrieval (Amy N. Langville, Carl D. Meyer)
Wikipedia: HITS algorithm

まずおさらいですが、PageRankの発想は、「重要なページからリンクされているページは重要」というものでした。
そして、各ページはそれぞれ一つのスコア(PageRank)を持ちます。
PageRankの特徴として、リンクが増えると、リンクされている側のページのスコアは上がりますが、
リンク元のページにはなんら恩恵がありません。

しかし実際、優良なページに多くのリンクを貼っているのであれば、そのページも便利なページではあります。いわゆるリンク集やナビサイトです。
この、優良なページにたどり着くことを容易にするページも評価しようとしているのが、HITSアルゴリズムです。
HITSアルゴリズムは、それぞれのページに Hub(ハブ値) と Authority(権威値) という二つのスコアを付与します。
Authority の方が、PageRankに近い概念で、Hubの方は、優良なページにリンクを飛ばすと高くなる値になります。

実際の計算式に近い形でまとめて説明すると、HITSアルゴリズムは次の二つの要素からなります。
– Hubが高いページからリンクされるほど、Authorityが高くなる。
– Authorityが高いページへリンクするほど、Hubが高くなる。

ここ最近の固有ベクトル中心性やPageRankの記事を読んでいただけていたら予想がつくと思うのですが、
これらの計算も行列の掛け算の繰り返しが収束することによって求まります。
そして、行列の固有ベクトルとして算出することもできます。

まず、$i$番目のノードから$j$番目のノードにリンクがある時に$(i, j)$成分が$1$に、そうでない時に$0$になる隣接行列を$L$とおきます。
数式で書くと以下の通りです。
$$
\mathbf{L} = \{a_{i, j}\} =
\left\{ \begin{align}1 (iからjにリンク有り)\\0 (iからjにリンク無し)\end{align}\right.
$$
(文献によって、定義が転置していたり、値が正規化されていたりするのでご注意ください。)

そして、それぞれのノードのハブ値のベクトル$\mathbf{h}^{(k)}$と、権威値のベクトル$\mathbf{a}^{(k)}$を次のように初期化します。
$\mathbf{1}$は全ての要素が1のベクトル、$N$はノード数です。
$$
\mathbf{h}^{(0)} = \mathbf{a}^{(0)} = \mathbf{1}/N.
$$

定義に沿って、ハブ値と、権威値を再帰的に計算するには、次の操作を繰り返すことになります。($\cdot$は行列積です)
$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{h}^{(k-1)} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{a}^{(k-1)} \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$

さて、numpyでこの通り実装し、ループを回して計算すると$\mathbf{h}^{(k)}$も$\mathbf{a}^{(k)}$も一定値に収束することは容易に観測されます。
一応、ランダムに生成したグラフに対して、上の数式の通りに計算して確認しておきましょう。

import numpy as np
import networkx as nx

# ランダムに有向グラフ生成
G = nx.random_graphs.fast_gnp_random_graph(n=10, p=0.2, directed=True)

# 隣接行列取得
L = nx.to_numpy_array(G)
print(L)
"""
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 1. 0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 1. 1. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [1. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 1. 0. 1. 0. 0.]
 [1. 0. 0. 0. 0. 1. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 1. 0. 1. 0. 0. 0.]]
"""
# ハブ値と権威値を初期化
hubs = np.ones(shape=nx.number_of_nodes(G))/nx.number_of_nodes(G)
authorities = np.ones(shape=nx.number_of_nodes(G))/nx.number_of_nodes(G)

# 再帰的に計算する。
for _ in range(40):
    # ハブ値から権威値を計算する。
    authorities = hubs @ L
    # 権威値からハブ値を計算する。
    hubs = authorities @ L.T

    # 標準化
    hubs /= sum(hubs)
    authorities /= sum(authorities)
    print("authorities: ", authorities.round(3))
    print("hubs:", hubs.round(3))
"""
authorities:  [0.105 0.    0.105 0.105 0.158 0.158 0.053 0.158 0.105 0.053]
hubs: [0.    0.156 0.156 0.067 0.067 0.089 0.2   0.156 0.022 0.089]
authorities:  [0.097 0.    0.097 0.124 0.142 0.204 0.035 0.168 0.124 0.009]
hubs: [0.    0.172 0.168 0.057 0.068 0.079 0.208 0.172 0.004 0.072]
authorities:  [0.097 0.    0.097 0.131 0.13  0.213 0.028 0.172 0.131 0.001]
hubs: [0.    0.178 0.175 0.052 0.069 0.078 0.207 0.178 0.001 0.063]

-- (中略) --

authorities:  [0.1   0.    0.1   0.138 0.116 0.216 0.021 0.172 0.138 0.   ]
hubs: [0.    0.183 0.18  0.047 0.069 0.081 0.203 0.183 0.    0.055]
authorities:  [0.1   0.    0.1   0.138 0.116 0.216 0.021 0.172 0.138 0.   ]
hubs: [0.    0.183 0.18  0.047 0.069 0.081 0.203 0.183 0.    0.055]
"""

この、最後の方で収束している値が、この記事のテーマのハブ値と権威値です。
Networkxで計算することもできるので見ておきましょう。
PageRank同様に複数の実装がありますが、 numpyで実装された、hits_numpyを使えば十分でしょう。

h, a = nx.hits_numpy(G)
print(h)
"""
{0: 0.0,
 1: 0.1828404557137138,
 2: 0.18031994425802442,
 3: 0.04654212497804568,
 4: 0.06918950852466288,
 5: 0.08062191959815146,
 6: 0.20269591155066588,
 7: 0.1828404557137138,
 8: 0.0,
 9: 0.054949679663021944}
"""
print(a)
"""
{0: 0.1000629943543116,
 1: -0.0,
 2: 0.10006299435431144,
 3: 0.13792829814529123,
 4: 0.11553047637984128,
 5: 0.21586948330461359,
 6: 0.020869885042915804,
 7: 0.17174757027342366,
 8: 0.1379282981452913,
 9: -0.0}
"""

さて、例によって、再帰的に計算して、収束を待つというのは非常にコストの高い計算なので、もう少し効率化を考えます。
先ほどの計算式をよく見ると、$\mathbf{h}^{(k)}$と$\mathbf{a}^{(k)}$は相互に計算するのではなく、
自分自身の前の状態から計算できることがわかります。少し変形するとこうですね。

$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{a}^{(k-2)} \cdot L^{\top} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{h}^{(k-2)} \cdot L \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$

$k=0$から計算が始まるので、この式からは偶数番目の項しか出てきませんが、収束先は同じですので無視してしまって、次の漸化式の収束先を考えましょう。
$$
\begin{align}
&\mathbf{a}^{(k)} = \mathbf{a}^{(k-1)} \cdot L^{\top} \cdot L,\\
&\mathbf{h}^{(k)} = \mathbf{h}^{(k-1)} \cdot L \cdot L^{\top},\\
&\mathbf{a}^{(k)}と、\mathbf{h}^{(k)}を正規化する.
\end{align}
$$

すると、固有ベクトル中心性やPageRank時と同じように、$\mathbf{h}^{(k)}$も$\mathbf{a}^{(k)}$も、その収束先を、
行列の最大固有値に対する固有ベクトルとして算出できます。
具体的には、
ハブ値$\mathbf{h}^{(k)}$のほうは、 $(L \cdot L^{\top})^{\top} = L \cdot L^{\top}$ の固有ベクトル、
権威値$\mathbf{a}^{(k)}$のほうは、 $(L^{\top} \cdot L)^{\top} = L^{\top} \cdot L$ の固有ベクトル、
として、求まります。

hub_eig = np.linalg.eig(L@L.T)[1][:, 0]
hub_eig /= sum(hub_eig)
print(hub_eig.round(3))
# [0.    0.183 0.18  0.047 0.069 0.081 0.203 0.183 0.    0.055]

authority_eig = np.linalg.eig(L.T@L)[1][:, 0]
authority_eig /= sum(authority_eig)
print(authority_eig.round(3))
# [ 0.1   -0.     0.1    0.138  0.116  0.216  0.021  0.172  0.138 -0.   ]

バッチリ算出できました。固有ベクトル本当に便利ですね。

最後に、ノードのサイズとして両指標を可視化しておきましょう。
比較用にPageRankと媒介中心性も入れました。

import matplotlib.pyplot as plt

# ハブ値と権威値算出
h_dict, a_dict = nx.hits_numpy(G)
h_list = np.array([h_dict[n] for n in G.nodes])
a_list = np.array([a_dict[n] for n in G.nodes])

# PageRankと媒介中心性も算出
pr_dict = nx.pagerank_numpy(G)
pr_list = np.array([pr_dict[n] for n in G.nodes])
bc_dict = nx.betweenness_centrality(G)
bc_list = np.array([bc_dict[n] for n in G.nodes])

# 可視化
fig = plt.figure(figsize=(12, 12), facecolor="w")
ax = fig.add_subplot(221, title="HITS: hubs")
nx.draw_networkx(G, pos=pos, node_size=3000*h_list, ax=ax, node_color="c")
ax = fig.add_subplot(222, title="HITS: authorities")
nx.draw_networkx(G, pos=pos, node_size=3000*a_list, ax=ax, node_color="c")
ax = fig.add_subplot(223, title="PageRank")
nx.draw_networkx(G, pos=pos, node_size=3000*pr_list, ax=ax, node_color="c")
ax = fig.add_subplot(224, title="betweenness centrality")
nx.draw_networkx(G, pos=pos, node_size=3000*bc_list, ax=ax, node_color="c")

PageRankではほとんど評価されていない1番のノードが、Hubとしてきちんと評価されていること、
それによって1番からリンクを得ている、2,3,5が、PageRankに比べて、権威値が高くなっていることなど確認できますね。

実験する前は PageRank と 権威値 はもっと似てる結果になると思っていたのですが、
(確かに似てはいるけど) 予想よりも指標の特徴がいろいろ出ていますね。