matplotlibでSurface plots

昨日に続いてmatplotlibの3次元グラフの話です。
今回のテーマは Surface plots。(日本語では表面プロットでいいのかな？)
２変数関数の可視化等に便利なやつですね。

ドキュメントは今回もこちら。 : The mplot3d Toolkit

今回は例として 鞍点を持つ次の関数を可視化してみましょう。
$$
z = f(x, y) = x^2 – y^2.
$$

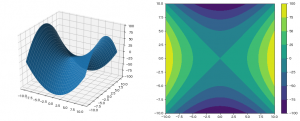
比較用に等高線で可視化したグラフと並べてみました。
参考: matplotlibで等高線

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


def f(x, y):
    return x**2 - y**2


X, Y = np.meshgrid(
        np.linspace(-10, 10, 101),
        np.linspace(-10, 10, 101),
    )
Z = f(X, Y)

fig = plt.figure(figsize=(16, 6), facecolor="w")
ax_3d = fig.add_subplot(121, projection="3d")
ax_3d.plot_surface(X, Y, Z)

ax = fig.add_subplot(122)
contour = ax.contourf(X, Y, Z)
fig.colorbar(contour)
plt.show()

結果はこちら。

可視化する対象によって向き不向きがあるのでいつもそうだというわけではないのですが、
今回のサンプルでは圧倒的に3次元プロットの方が圧倒的に関数の形をつかみやすいですね。