思いのほか理論編が長くなってしまいすでにインパルス応答で4記事目ですが、ようやく実装の話です。
グレンジャー因果性と同様に、statsmodelsで学習したVARモデルはインパルス応答関数のメソッドも持っています。
メソッド名は irf です。
早速やってみましょう。
モデルは、直交化インパルス応答関数の計算例の記事と同じです。
サンプルデータの生成と、パラメーターの推定まで完了しているとします。
今回は次の状態になりました。
# 学習したモデルのパラメーター
result = model.fit(maxlags=1)
print(result.summary())
"""
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Sun, 23, Feb, 2020
Time: 21:45:36
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 0.924001
Nobs: 99.0000 HQIC: 0.830357
Log likelihood: -312.903 FPE: 2.15278
AIC: 0.766721 Det(Omega_mle): 2.02800
--------------------------------------------------------------------
Results for equation y1
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 0.177695 0.918241 0.194 0.847
L1.y1 0.553623 0.112916 4.903 0.000
L1.y2 0.169688 0.169945 0.998 0.318
========================================================================
Results for equation y2
========================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------
const 1.306800 0.408504 3.199 0.001
L1.y1 0.085109 0.050234 1.694 0.090
L1.y2 0.760450 0.075605 10.058 0.000
========================================================================
Correlation matrix of residuals
y1 y2
y1 1.000000 0.629788
y2 0.629788 1.000000
"""
サマリーの最後に、撹乱項の相関行列がありますが、分散共分散行列がみたいのでそちらも表示しておきましょう。
sigma_uに入ってます。
# 分散共分散行列
print(result.sigma_u)
"""
[[4.12100608 1.1546159 ]
[1.1546159 0.81561201]]
"""
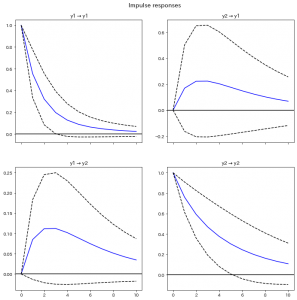
さて、まずは非直行化インパルス応答関数を計算して可視化してみましょう。
ちなみに、直行化/非直行化を指定するのは可視化(plot)の引数であり、計算時点で両方とも算出されています。
import matplotlib.pyplot as plt
# 10期先までの非直交化インパルス応答関数のプロット
period = 10
irf = result.irf(period)
irf.plot()
plt.show()
結果がこちらです。
想定通りの結果になっていますね。
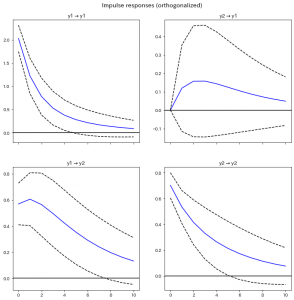
続いて、(直行化)インパルス応答関数です。
用語としては、単にインパルス応答関数と言ったら、直行化の方をさすのですが、ライブラリでは明示的に、
orth=Trueを指定しなければなりません。(デフォルトはFalse)
計算は完了しているので、可視化のみです。
irf.plot(orth=True)
plt.show()
結果がこちら。
0期先の値が特徴的で、 y2からy1へは影響していないのに、y1からy2へは影響が発生していますね。
また、もう一点注意しないといけない点があります。
非直行化の方は、y1からy1 および y2からy2への0期先の影響の値が1であることから分かる通り、
1単位のショックを与えた時のインパルス応答関数を計算されていました。
しかし、直行化の方は、そうではなく、1標準偏差のショックを与えた時のインパルス応答関数の値になっています。
(この辺の挙動はドキュメントのどこに書いてあるのだろう?)
結果をプロットするのではなく、値を利用したい場合もあると思います。
その場合、次の2変数にプロットされた値がそれぞれ入っていますのでこれが使えます。
irf.irfs
irf.orth_irfs