対数正規分布の話の続きです。
参考: 前回の記事
Pythonで対数正規分布を扱う場合、(もちろんスクラッチで書いてもいいのですが普通は)Scipyに実装されている、
scipy.stats.lognormを使います。
これに少し癖があり、最初は少してこずりました。
まず、対数正規分布の確率密度関数はパラメーターを二つ持ちます。
次の式の$\mu$と$\sigma$です。
$$
f(x) =\frac{1}{\sqrt{2\pi}\sigma x}\exp\left(-\frac{(\log{x}-\mu)^2}{2\sigma^2}\right).
$$
それに対して、scipy.stats.lognorm の確率密度関数(pdf)は、
s, loc, scale という3つのパラメーターを持ちます。 ややこしいですね。
正規分布(scipy.stats.norm)の場合は、 loc が $\mu$に対応し、scaleが$\sigma$に対応するので、とてもわかりやすいのですが、lognormはそうはなっていなっておらず、わかりにくくなっています。
(とはいえ、ドキュメントには正確に書いてあります。)
Scipyの対数正規分布においては、確率密度関数は
$$
f(x, s) = \frac{1}{sx\sqrt{2\pi}}\exp\left(-\frac{\log^2{x}}{2s^2}\right)
$$
と定義されています。
そして、$y=(x-loc)/scale$と変換したとき、lognorm.pdf(x, s, loc, scale) は、 lognorm.pdf(y, s) / scale と等しくなります。(とドキュメントに書いてあります。)
わかりにくいですね。
$\mu$と$\sigma$とはどのように対応しているのか気になるのですが、上の2式を見比べてわかるとおり、(そしてドキュメントにも書いてある通り、)
まず、引数のsが、パラメーターの$\sigma$に対応します。 (scaleじゃないんだ。)
そして、引数のscaleは$e^{\mu}$になります。(正規分布の流れで、locと$\mu$が関係してると予想していたのでこれも意外です。)
逆にいうと、$\mu=\log{scale}$です。
locはまだ登場していませんが、一旦ここまでの内容をプログラムで確認しておきます。
lognorm(s=0.5, scale=100) とすると、 $\sigma=0.5$で、$\mu=\log{100}\fallingdotseq 4.605$の対数正規分布になります。
乱数をたくさん取って、その対数が、期待値$4.605…$、標準偏差$0.5$の正規分布に従っていそうかどうかみてみます。
from scipy.stats import lognorm
import matplotlib.pyplot as plt
import numpy as np
data = lognorm(s=0.5, scale=100).rvs(size=10000)
log_data = np.log(data)
print("対数の平均:", log_data.mean())
# 対数の平均: 4.607122120944554
print("対数の標準偏差:", log_data.std())
# 対数の標準偏差: 0.49570170767616645
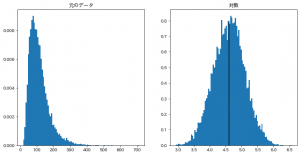
fig = plt.figure(figsize=(12, 6), facecolor="w")
ax = fig.add_subplot(1, 2, 1, title="元のデータ")
ax.hist(data, bins=100, density=True)
ax = fig.add_subplot(1, 2, 2, title="対数")
ax.hist(log_data, bins=100, density=True)
# 期待値のところに縦線引く
ax.vlines(np.log(100), 0, 0.8)
plt.show()
出力された図がこちらです。
想定通り動いてくれていますね。
残る loc ですが、 これは分布の値を左右に平行移動させるものになります。
先出の$y=(x-loc)/scale$ を $x = y*scale + loc$ と変形するとわかりやすいかもしれません、
わかりやすくするために、locに極端な値($\pm 1000$と$0$)を設定して、乱数をとってみました。
(sとscaleは先ほどと同じです。)
locs = [-1000, 0, 1000]
fig = plt.figure(figsize=(18, 6), facecolor="w")
for i, loc in enumerate(locs, start=1):
data = lognorm(s=0.5, scale=100, loc=loc).rvs(size=1000)
ax = fig.add_subplot(1, 3, i, title=f"loc={loc}")
ax.hist(data, bins=100, density=True)
plt.show()
出力がこちらです。
分布の左端が それぞれ、locで指定した、 -1000, 0, 1000 付近になっているのがみて取れると思います。