以前、ARモデルの推定をstatsmodelsで行う方法を書きました。
pythonでARモデルの推定
今回行うのははARMAモデルの推定です。
結果に表示されるconstが、予想してた値にならず結構苦戦しました。
これ、ARモデルと仕様が違って、定数項ではなく過程の期待値が返されるんですね。
密かにライブラリのバグじゃ無いのかと思ってます。ちなみに バージョンはこれ。
$ pip freeze | grep statsmodels
statsmodels==0.9.0
ドキュメントはこちら
statsmodels.tsa.arima_model.ARMA
ARモデルとは使い方が色々と異なります。
例えば、ARモデルでは、次数を推定する関数(select_order)をモデルが持っていましたが、
ARMAモデルにはなく、
arma_order_select_ic
という別のところ(stattools)に準備された関数を使います。
今回もARMA過程を一つ固定し、データを準備して行いますが、過程の次数が大きくなるとなかなか上手くいかないので、
ARMA(1, 1)過程のサンプルを作りました。
$$
y_t = 50 + 0.8y_{t-1} + \varepsilon_{t} + 0.4\varepsilon_{t-1} \\
\varepsilon_{t} \sim W.N.(2^2)
$$
この過程の期待値は $50/(1-0.8)=250$です。
それではデータの生成から行います。
T = 200
phi_1 = 0.8
theta_1 = 0.4
c = 50
sigma = 2
# 過程の期待値
mu = c/(1-phi_1)
# 撹乱項生成
epsilons = np.random.normal(0, sigma, size=T)
arma_data = np.zeros(T)
arma_data[0] = mu + epsilons[0]
for t in range(1, T):
arma_data[t] = c+phi_1*arma_data[t-1]+epsilons[t]+theta_1*epsilons[t-1]
# データを可視化し、定常過程である様子を見る (記事中では出力は略します)
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 1, 1)
ax.plot(y)
plt.show()
これで検証用データが作成できましたので、
早速ARMAモデルを構築して係数と撹乱項の分散がもとまるのかやってみましょう。
今回も次数の決定にはAIC基準を使いました。
# 次数の推定
print(sm.tsa.arma_order_select_ic(arma_data, max_ar=2, max_ma=2, ic='aic'))
# 結果
'''
{'aic': 0 1 2
0 1107.937296 920.311164 1341.024062
1 844.276284 818.040579 820.039660
2 821.624647 820.039106 821.993934, 'aic_min_order': (1, 1)}
'''
# ARMAモデルの作成と推定
arma_model = sm.tsa.ARMA(y, order=(1, 1))
result = arma_model.fit()
最後に結果を表示します。
# 結果の表示
print(result.summary())
# 出力
'''
ARMA Model Results
==============================================================================
Dep. Variable: y No. Observations: 200
Model: ARMA(1, 1) Log Likelihood -416.830
Method: css-mle S.D. of innovations 1.937
Date: Thu, 11 Apr 2019 AIC 841.660
Time: 00:18:59 BIC 854.853
Sample: 0 HQIC 846.999
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 251.5200 0.866 290.374 0.000 249.822 253.218
ar.L1.y 0.7763 0.049 15.961 0.000 0.681 0.872
ma.L1.y 0.4409 0.067 6.622 0.000 0.310 0.571
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.2882 +0.0000j 1.2882 0.0000
MA.1 -2.2680 +0.0000j 2.2680 0.5000
-----------------------------------------------------------------------------
'''
自己回帰モデル部分のラグ1の係数が0.7763 (正解は0.8)、
移動平均モデル部分のラグ1の係数は0.4409 (正解は0.4)なので、そこそこ正しいですね。
撹乱項の標準偏差(S.D. of innovations) も 1.937となり、正解の2に近い値が得られています。
constには50に近い値になるはずだと思っていたのですが、
ここは過程の式の定数項ではなく期待値が出力されるようです。
公式ドキュメント内で該当の説明を見つけることができていませんが、
色々なモデルで検証したのでおそらく間違い無いでしょう。
また、次の関数を使って、元のデータとモデルの予測値をまとめて可視化できます。
result.plot_predict()
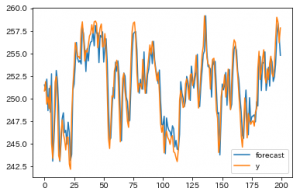
今回のモデルは非常に予測しやすいものを例として選んだので、大体近しい値になっていますね。
