※この記事では dtreevizの version 0.8.2 を使っています。
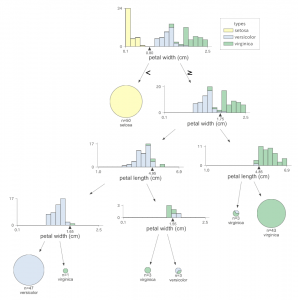
前回の記事では、dtreeviz を使って学習済みの決定木を可視化しました。
dtreevizではこの他にも、1個か2個の特徴量とラベルの関係を可視化できます。
それが、 ctreeviz_univar と、ctreeviz_bivar です。
扱える特徴量がuniの方が1個、biの方が2個です。
データは必要なので、irisを読み込んでおきます。今回は木は不要です。
(その代わり、max_depsかmin_samples_leafのどちらかの設定が必須です。)
from sklearn.datasets import load_iris
iris = load_iris()
まず1個のほうをやってみます。
特徴量4個しかないので全部出します。
import matplotlib.pyplot as plt
from dtreeviz.trees import ctreeviz_univar
figure = plt.figure(figsize=(13, 7), facecolor="w")
for i in range(4):
ax = figure.add_subplot(2, 2, i+1)
ctreeviz_univar(
ax,
iris.data[:, i],
iris.target,
max_depth=2,
feature_name=iris.feature_names[i],
class_names=iris.target_names.tolist(),
target_name='types'
)
plt.tight_layout()
plt.show()
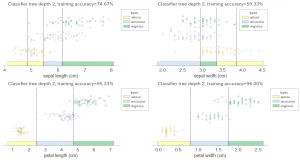
どの特徴量が有効なのか、自分的にはこれまでで一番わかりやすいと感じました。
次は2個の方です。特徴量2種類とラベルを渡すと、それらの関係を可視化してくれます。
2個ずつ選んで2つのグラフで可視化してみました。
引数、ですがfeature_name が feature_names になっており、渡す値も文字列が配列になっているので注意が必要です。
from dtreeviz.trees import ctreeviz_bivar
figure = plt.figure(figsize=(5, 12), facecolor="w")
ax = figure.add_subplot(2, 1, 1)
ctreeviz_bivar(
ax,
iris.data[:, :2],
iris.target,
max_depth=2,
feature_names=iris.feature_names[:2],
class_names=iris.target_names.tolist(),
target_name='types'
)
ax = figure.add_subplot(2, 1, 2)
ctreeviz_bivar(
ax,
iris.data[:, 2:],
iris.target,
max_depth=2,
feature_names=iris.feature_names[2:],
class_names=iris.target_names.tolist(),
target_name='types'
)
plt.show()
出力がこちら。
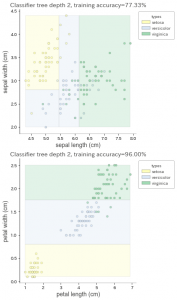
これもわかりやすいですね。