Python(と jupyter notebook)でデータを可視化する場合、色を16進法のRGBで指定できるライブラリは多くあります。
Matplotlibがベースになっているものは、そのカラーマップを指定できることも多いのですし、
「rは赤」、「bは青」など一部の色はアルファベットや色名で指定できるのですが、
もっと多くの色を使いたかったり、値によってグラデーションをつけたい場合で逐一RGBを構築するのは結構な手間です。
そこで、Matplotlibの配色をそのまま流用できないかと思って調べてみました。
結論から言うと、結構簡単に使えそうです。
まず、配色そのもののデータは、
matplotlib.cm と言うモジュールに含まれています。
配色はその名前で指定しますが、名前と実際の色の対応はこちらのリファレンスをみると良いでしょう。
Colormap reference
使いたいカラーマップが決まったら、cm.get_cmap() か、 cmの属性として、使うことができます。
要するに次の2行は同じものです。
cm.get_cmap("Greens")
cm.Greens
さて、どちらもカラーマップのオブジェクトを返してくれますが、
そのカラーマップのオブジェクトにに数値を渡すと、RGBのタプルを返してくれます。
import matplotlib.cm as cm
print(cm.get_cmap("Greens")(0.7, alpha=0.5))
# (0.18246828143021915, 0.5933256439830834, 0.3067589388696655, 0.5)
print(cm.get_cmap("Paired")(3))
# (0.2, 0.6274509803921569, 0.17254901960784313, 1.0)
渡す数値ですが、連続的に色が変化するものには、 0〜1の値を渡します。
色の値が不連続な(要はリファレンスで、Qualitativeのカテゴリにあるもの)は、0〜1の値で渡しても大丈夫ですが、
整数値で0,1,2,3などを指定しても大丈夫です。
これらは、1と1.0や2と2.0など、同じ値でも整数型と浮動小数型で結果が変わるので注意してください。
ちなみに、値はリスト形式で複数同時に渡しても大丈夫です。
さて、最初の話に戻りますが、このRGB値のタプルを他のライブラリ等で使うには、16進法の文字列に変換する必要があります。
255倍して16進法の文字列に変化して、シャープをつけて結合するコードを自分で書いてもいいのですが、
なんと Matplotlibにその関数が用意されていました。
matplotlib.colors.rgb2hex です。
これはなぜか、色のリストは受け取ってくれないので、順番に適用していかないといけないのですが、
RGBのタプルを16進法文字列に手軽に変換してくれます。
(keep_alpha=Trueを指定すると透明度も含めてくれます。デフォルトはFalseです。)
試しにカラーマップから10色取り出してみましょう。
import matplotlib.colors as mcolors
import matplotlib.cm as cm
import numpy as np
cmap = cm.get_cmap("BuGn")
for rgb in cmap(np.arange(0, 1, 0.1)):
print(mcolors.rgb2hex(rgb))
"""
#f7fcfd
#e9f7fa
#d6f0ee
#b8e4db
#8fd4c2
#65c2a3
#48b27f
#2f9858
#157f3b
#006428
"""
10個の色が取り出せましたね。
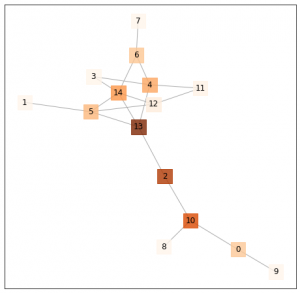
最後に何か例を出しておきたいので、networkx で作成したグラフに中心性で色をつけてみました。
(グラフの中心性には複数の種類がありますが、今回は媒介中心性を使いました。)
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as mcolors
while True:
# ランダムにグラフを生成する
G = nx.random_graphs.fast_gnp_random_graph(15, 0.2)
# 連結なグラフが生成できたらループを抜ける
if nx.is_connected(G):
break
# 媒介中心性の計算
centrality = nx.betweenness_centrality(G)
# 辞書形式なので、ノードの順番と揃えてリスト化する。
centrality_list = np.array([centrality[node] for node in G.nodes])
# 媒介中心性を0〜1に正規化する
color_level = centrality_list - min(centrality_list)
color_level/=max(color_level)
# ノードの色の生成
rgb_list = cm.get_cmap("Oranges")(color_level, alpha=0.8)
node_color=[mcolors.rgb2hex(rgb, keep_alpha=True) for rgb in rgb_list]
# グラフの可視化
fig = plt.figure(figsize=(8, 8), facecolor="w")
ax = fig.add_subplot(1,1,1)
nx.draw_networkx(
G,
node_color=node_color,
node_size=500,
edge_color="#aaaaaa",
node_shape="s"
)
出力がこちら。
媒介中心性が高いところが色が濃くなっているのがわかります。