カテゴリー: 統計学

Scipyが使える今となっては使う機会はほぼありませんが、
一様分布から正規分布に従う乱数を作成できる方法である、ボックス＝ミュラー法(Box–Muller’s method)を紹介します。

正規分布は累積分布関数やその逆関数が初等関数では表現できず、
最近紹介した逆関数法で乱数を生成するのは少々困難です。

そこでこのボックス＝ミュラー法が使われます。
参考:自然科学の統計学(東京大学出版会)の 11.3 正規乱数の発生法

まず、確率変数$X$,$Y$が互いに独立で、共に$(0,1)$上の一様分布に従うとします。
この時、
$$
\begin{align}
Z_1 & = \sqrt{-2\log{X}}\cos{2\pi Y},\\
Z_2 & = \sqrt{-2\log{X}}\sin{2\pi Y}
\end{align}
$$
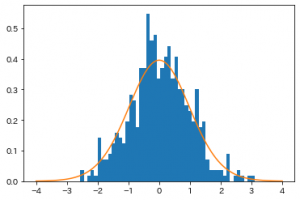
とすると、$Z_1$と$Z_2$は標準正規分布$N(0,1)$に従う互いに独立な確率変数になります。

厳密な証明は今回は省略します。
ただ、数式をみれば、正規分布の確率密度関数が指数関数の形をしているので$\log$が出てくるのも、
円周率も出てくるなど円に関係しそうな気配があるので三角関数が出てくるのもなんとなく納得性があります。

ただ、「互いに独立な」ってのは正直驚きます。
$Z_1^2+Z_2^2=-2\log{X}$って関係式が成り立つのに独立ってことはないんじゃないかと思えますね。　
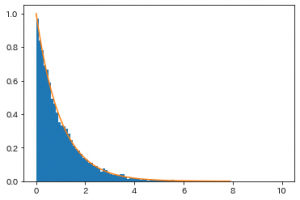
(この$X$が定数ではないのがキモで、$0<X<1$から、$-2\log{X}$が
非常に大きな値も含めて実に自由に動くので独立性が生まれるようです。)

ここだけ実験して相関係数が0に近いことを確認しておきましょう。

import numpy as np

# 一様分布に従うX, Yをそれぞれ10000個生成
X = np.random.rand(10000)
Y = np.random.rand(10000)

# Z_1, Z_2 を計算
Z_1 = np.sqrt(-2*np.log(X))*np.cos(2*np.pi*Y)
Z_2 = np.sqrt(-2*np.log(X))*np.sin(2*np.pi*Y)

# 相関係数を算出
print(np.corrcoef(Z_1, Z_2)[0, 1])
# -0.0043281961119066865

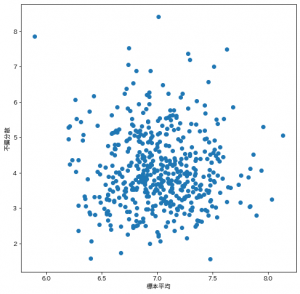
確かに独立っぽいですね。
散布図等も出してみましたが何か特別な関係性は見当たらないようです。

前回の記事で逆関数法を紹介したので具体的な分布で試そうという趣旨の記事です。
今回は指数分布を使います。(累積分布関数もその逆関数も容易に計算できるから)

まず、指数分布の確率密度関数から。指数分布はパラメータ$\lambda$を一つ持ちます。
$$
f(x) = \left\{
\begin{matrix}
\lambda e^{-\lambda x} & (x \leq 0)\\
0 & (x < 0) \end{matrix} \right. $$ そして、累積分布関数は次のようになります。 $$ F(x) = \left\{ \begin{matrix} 1-e^{-\lambda x} & (x \leq 0)\\ 0 & (x < 0) \end{matrix} \right. $$ さらにその逆関数は、こうなります。 $$ F^{-1}(u) = - \frac{1}{\lambda}\log(1-u) \quad (0\leq u <1). $$ それではPythonで、$[0,1)$の乱数を10000個くらい生成して、 逆関数法で$f(x)$に従う乱数が得られるのか実験してみましょう。 今回は単純のため、$\lambda=1$とします。 Pythonでやってみたコードと結果がこちら。

import numpy as np
import matplotlib.pyplot as plt

# 標準一様分布　に従う乱数を10000個生成する
U_data = np.random.rand(10000)
# 逆関数方法で指数分布に従うデータ生成
result_data = -np.log(1 - U_data)
# ヒストグラムと確率密度関数をプロットする
fig = plt.figure(facecolor="w")
ax = fig.add_subplot(111)
ax.hist(result_data, bins=100, density=True)
ax.plot(np.arange(0, 8, 0.1), np.exp(-1*np.arange(0, 8, 0.1)))
plt.show()

出力。

データ件数が多いので非常に綺麗に出ましたね。

学生時代にExcelで色々シミュレーションしていたときによく使った方法です。
エクセル関数で生成できる乱数がrand()で得られる一様分布の乱数くらいしかなく、
他の分布に従う乱数が欲しい時はそこから変換して作っていました。
(Pythonを使うようになってから、Scipyに実装されている確率分布を使えば良いので、滅多に行うことがなくなりました。)

ただ、逆関数法という名前がついていることは最近知りました。
逆関数法 出典: フリー百科事典『ウィキペディア（Wikipedia）』
英語では inverse transform sampling というようです。

前回の記事同様、少々厳密性は犠牲にして、登場する各関数等は(連続性や滑らかさなどの)適切な仮定を満たしているものとします。

まず前提として、区間$[0,1]$上の一様分布に従う乱数$U$は取得できるものとします。
$$
\begin{align}
f_U(u) = \left\{\begin{matrix}
1& u \in[0,1]\\
0& u \notin[0,1]
\end{matrix}\right.
\end{align}
$$

そして欲しい乱数$X$が従う確率密度関数を$f(x)$とし、累積分布関数を$F(x)$とします。
$$
F(x) = \int_{-\infty}^x f(y) dy.
$$

そして$F$の逆関数を$F^{-1}$とした時、
$X=F^{-1}(U)$は、確率密度関数$f(x)$に従う確率変数となります。

証明は前回の記事で紹介した、確率変数の変換を使います。
この記事中の、$g$に相当するのが$F^{-1}$であることに注意して計算します。
まず前回の記事で紹介した返還式に、この記事中で使っている記号に注意しながら代入します。
$$
f_X(x) = f_U(F(x))\frac{du}{dx}.
$$
ここで、累積分布関数の性質より$0\leq F(x)\leq 1$より、$f_U(F(x))=1$です。
さらに、
$$
\frac{du}{dx} = \frac{d}{dx}F(x) = f(x)
$$
となることから、次の式が示されました。
$$
f_X(x) = f(x).
$$

累積分布関数(と、その逆関数)が具体的に計算できる確率分布についてはこれは非常に便利な式です。
学生時代は個人的な調べ物のため、指数分布を使うシミュレーションをよくやっていたので、よく使っていました。

対応関係にある確率変数について、一方の確率変数が従う確率分布が分かっているときに、
もう一方の確率変数が従う確率分布を求める方法の紹介です。
大抵の統計学の教科書のかなり前半の方に登場しますし、色々な確率分布の導出などにも使うので、
非常に基本的な内容ですが、意外に知名度が低いように感じています。

早速必要な記号の定義から始めましょう。
二つの確率変数$X$と$Y$が、それぞれ確率密度関数$f_X(x)$と$f_Y(y)$の確率分布に従っているとします。
さらに、$X$と$Y$の間に$y=g(x)$という1対1の対応があると仮定します。

($\frac{dx}{dy}$を使うので、$g$の微分可能性の条件なども必要なはずなのですが、
この辺りは統計学の教科書でもあまり重要視されてないような気がします。
とりあえずこの記事では必要な仮定は満たされているものとします。)

このとき、次の式が成り立ちます。
$$
f_Y(y) = f_X(g^{-1}(y))\frac{dx}{dy}.
$$

証明と呼ぶにはかなり荒い説明になるのですが、自分は次のよう理解しています。
(式をど忘れしたときにさっと導出するため、厳密性は犠牲にしていますのでご注意をお願いします。
例えば、積分した結果が等しいからといって即座に中の関数が等しいことの証明にはならないと思います。)

まず、XとYの対応関係(y=g(x))から定数$a,b (a\leq b)$に対して次の等式が成り立ちます。
$$
P(a\leq Y \leq b) = P(g^{-1}(a)\leq X \leq g^{-1}(b)).
$$
これを確率密度関数の積分で表記すると次のようになります。
$$
\int_a^bf_Y(y)dy = \int_{g^{-1}(a)}^{g^{-1}(b)}f_X(x)dx.
$$
この右辺を$x=g^{-1}(y)$で置換積分すると、積分区間は$x:g^{-1}(a)\rightarrow g^{-1}(b)$に対して、$y:a\rightarrow b$となります。
よって、次のようになります。($dx/dy$のつけ忘れに注意。）
$$
\int_a^bf_Y(y)dy = \int_a^b f_X(g^{-1}(y))\frac{dx}{dy}dy.
$$
この積分の中の式を比較することで、上の確率密度関数の変換の公式を思い出すことができます。

最近数式ばかり増えてプログラムが登場してないのでちょっとした検証をやろうと思います。
今回行うのは、タイトルにある通り、標本平均と不偏分散の独立性です。

少し前の母平均の区間推定のところで、
$\sqrt{n}(\bar X-\mu)/s$は、自由度$n-1$の$t$分布に従う、とさらっと書きましたが、
これの前提になっているのが、
$\frac{\bar X -\mu}{\sigma/\sqrt{n}}$が標準正規分布に従うことと、
$\frac{(n-1)s^2}{\sigma^2}$が自由度$n-1$のカイ二乗分布に従うこと、
そして、この二つが独立であることです。
スチューデントの$t$分布の定義も参照。

この二つの値が独立であることって結構不思議な現象だと感じないでしょうか。
同じ標本から算出している値なので何か関係があっても良さそうです。

数式的に計算していって確かめることも可能なのですが、今回は乱数でいっぱい標本をとって、
プロットすることで確かに独立してるっぽいことを眺めて見たいと思います。

標本は$N(7, 2^2)$からとりました。サンプルサイズ$30$で、$500$回標本を取り、
標本平均と不偏分散の相関係数を算出し、散布図にプロットしています。

コードと結果がこちら。

import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm

mu = 7
sigma = 2
sample_size = 30
sample_count = 500

result_list = []
for i in range(sample_count):
    X = norm(loc=mu, scale=sigma).rvs(sample_size)
    mu_ = X.mean()
    var_ = X.var(ddof=1)
    result_list.append({"mu_":  mu_, "var_": var_})

result_df = pd.DataFrame(result_list)
print("相関係数:"+str(np.corrcoef(result_df.mu_, result_df.var_)[0, 1].round(3)))
# 相関係数:-0.021

fig = plt.figure(figsize=(8, 8), facecolor="w")
ax = fig.add_subplot(111)
ax.set_xlabel("標本平均")
ax.set_ylabel("不偏分散")
ax.scatter(result_df.mu_, result_df.var_)
plt.show()

出力された散布図がこちらです。

相関係数は確かに0に近いですし、散布図もいかにも無相関っぽい形になりました。

せっかくなので、各標本ごとに$t$値も算出して、$t$分布と見比べておきましょう。

import numpy as np
from scipy.stats import t

result_df["t_"] = np.sqrt(sample_size-1)*(result_df.mu_ - mu) / result_df.var_**0.5
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(result_df["t_"].values, bins=50, density=True)
ax.plot(np.linspace(-4, 4, 101), t(sample_size-1).pdf(np.linspace(-4, 4, 101)))
plt.show()

出力がこちら。

だいたいフィットしてそうですね。

前回の記事で正規分布のモーメント母関数を算出しましたので、それを使って何かやろうとした記事です。
参考:正規分布のモーメント母関数を導出する

尖度の記事で、尖度の定義を紹介した時、
正規分布の尖度が0となるように3を引いた定義を紹介しました。
これは当然正規分布の期待値周りの4次のモーメントを標準偏差の4乗で割った値(４次の標準化モーメント)が、
パラメーターによらず定数$3$であることを前提とします。
これを証明してみましょう。

さて、モーメント母関数の性質をそのまま使うとすると、まずは
$$
M_X(t) = e^{\mu t+\frac{\sigma^2}{2}t^2}.
$$
を4回微分する事になるのですが、やってみたらかなり手間がかかりました。
ということで少しだけ工夫します。

まず、標準化モーメントが期待値$\mu$に依存しないことをみます。
(式変形の途中で$x-\mu=y$ と置換しました。また、分母の$\sigma^4$は定数なので一旦無視します。)
$$
\begin{align}
E\left[(X-\mu)^4\right] &= \int_{-\infty}^{\infty}(x-\mu)^4\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\\
&= \int_{-\infty}^{\infty}y^4\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{y^2}{2\sigma^2}}dy\\
&= E\left[Y^4\right].
\end{align}
$$
よって、期待値が$0$の場合を考えれば良いことになります。
期待値が$0$、分散が$\sigma^2$の正規分布のモーメント母関数は、$M_X(t) = e^{\frac{\sigma^2}{2}t^2}$ですが、
これを4回微分するのも少々面倒なので、直接テイラー展開を計算します。

$$
\begin{align}
M_X(t) &= e^{\frac{\sigma^2}{2}t^2}\\
&=\sum_{n=0}^{\infty}\frac{1}{n!}(\frac{\sigma^2}{2}t^2)^n\\
&=\sum_{n=0}^{\infty}\frac{1}{n!}(\frac{\sigma^2}{2})^n t^{2n}.
\end{align}
$$
ここで、$t^4$の項に着目するわけですが、$\sum$の中の$t$の右肩に乗ってる指数部分が$2n$なので、着目するのは$n=2$の項です。
つまり
$$\frac{1}{2!}(\frac{\sigma^2}{2})^2 t^{4}.$$
少し整理してあげるとこうなります。
$$\frac{3\sigma^4}{4!}t^4.$$

ここから、次の式が言えて、$E[X^4] = 3\sigma^4$、少し変形して$E[\frac{X^4}{\sigma^4}] = 3$もわかります。

そして、この値が正規分布の期待値に依存しないことも先に示しているので、
一般の期待値$\mu$、分散$\sigma^2$の正規分布について、4次の標準化モーメントは、3であることが示されました。
$$
E\left[\frac{(X-\mu)^4}{\sigma^4}\right] = 3.
$$

正規分布は分散によって尖ったり平らになったりしてる印象があるのですが、
4次のモーメントによって定義される尖度という観点で見たら、尖り具合は常に一定ということですね。

前回の記事でモーメント母関数を紹介しましたので、具体的に一つ導出してみようと思います。
例に取り上げるのは一番重要な確率分布である正規分布です。
(難易度も易しすぎず難しすぎずで、しばらく手を動かして積分計算するような作業をやってない自分には良いリハビリでした。)

期待値$\mu$,分散$\sigma^2$の正規分布の確率密度関数は、次の式です。
$$
f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}.
$$

これをモーメント母関数の定義式に代入して計算していきましょう。
$$
\begin{align}
M_X(t) &= E\left[e^{tX}\right]\\
&= \int_{-\infty}^{\infty}e^{tx}f(x)dx\\
&= \int_{-\infty}^{\infty}e^{tx}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\\
&= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty}e^{-\frac{(x-\mu)^2}{2\sigma^2}+tx}dx.
\end{align}
$$
ここで積分の中の指数関数の指数部に着目します。
$$
\begin{align}
指数部 &= -\frac{(x-\mu)^2}{2\sigma^2}+tx\\
&= -\frac{1}{2\sigma^2}\{x^2-2\mu x+\mu^2-2\sigma^2tx\}\\
&= -\frac{1}{2\sigma^2}\{x^2-2(\mu+\sigma^2t)x+(\mu+\sigma^2t)^2-(\mu+\sigma^2t)^2+\mu^2\}\\
&= -\frac{1}{2\sigma^2}\{(x-(\mu+\sigma^2t))^2-(\mu+\sigma^2t)^2+\mu^2\}\\
&= -\frac{1}{2\sigma^2}\{(x-(\mu+\sigma^2t))^2-2\mu\sigma^2t-\sigma^4t^2\}\\
&= -\frac{1}{2\sigma^2}\{(x-(\mu+\sigma^2t))^2\}+\mu t+\frac{\sigma^2}{2}t^2.
\end{align}
$$
平方完成なんて久しぶりにやったので少し丁寧に書きましたが、計算するとこのように整理できます。
こちらを元の式に代入します。

$$
\begin{align}
M_X(t) &= \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{\infty}e^{-\frac{(x-(\mu+\sigma^2t))^2}{2\sigma^2}+\mu t+\frac{\sigma^2}{2}t^2}dx\\
&= e^{\mu t+\frac{\sigma^2}{2}t^2} \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-(\mu+\sigma^2t))^2}{2\sigma^2}}dx.
\end{align}
$$
ここで、積分の中にある次の部分に着目します。
$$
\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-(\mu+\sigma^2t))^2}{2\sigma^2}}.
$$
実はこれ、期待値$\mu+\sigma^2t$、分散$\sigma^2$の正規分布の確率密度関数に等しく、区間$[-\infty,\infty]$で積分すると$1$になります。

したがって、正規分布のモーメント母関数は次のように書けることが証明できました。
$$
M_X(t) = e^{\mu t+\frac{\sigma^2}{2}t^2}.
$$

前々回と前回の記事で、歪度と尖度という指標を紹介しましたが、
おなじみの期待値$\mu=E(X)$や、分散$\sigma^2=E(X^2)-E(X)^2$なども合わせて考えると、
確率分布の形は$E[(X-\mu)^r]$、もしくは$E[X^r]$によって決まってくることがわかります。

一般に、次の値をそれぞれ、原点まわりの$r$次のモーメント(moment)、$X$の期待値まわりの$r$次のモーメントと言います。
$$
\begin{align}
\mu_r &= E(X^r).\\
\mu_r^{\prime} &= E[(X-\mu)^r].
\end{align}
$$
実際に計算してみるとわかるのですが、rが大きくなるとこの計算を直接行うのは結構手間なことが多いです。

そこで、全ての次数のモーメントを成績できるモーメント母関数(moment generating function)と呼ばれる関数が考案されています。
それは次の式で定義されます。
$$
M_X(t) = E\left[e^{tX}\right].
$$
(ただし、確率分布によっては、期待値を求める無限和や積分が収束せず、存在しないこともあり得ます。)

このモーメント母関数を$r$回微分して、$t=0$と置いた導関数が、原点周りの$r$次のモーメントになります。
式で書くと、次のようになります。
$$
M_X^{(r)}(0)=\mu_r = E[X^r]
$$

これは、$e^{tX}$のテイラー展開、$e^{tX}=\sum_{n=0}^{\infty}(tX)^n/n!$と期待値の線形性からわかります。
実際代入して整理してみると、次のようになります。
$$
\begin{align}
M_X(t) &= E\left[e^{tX}\right]\\
&= E\left[\sum_{n=0}^{\infty}(tX)^n/n!\right]\\
&= \sum_{n=0}^{\infty}(E[X^n]/n!)t^n.
\end{align}
$$

これを両辺$r$回微分すると次のようになります。
$$
\begin{align}
M_X^{(r)}(t) &= \sum_{n=r}^{\infty}(E[X^n]/(n-r)!)t^{n-r}\\
&= E[X^r] + \sum_{n=r+1}^{\infty}(E[X^n]/(n-r)!)t^{n-r}.
\end{align}
$$
これに$t=0$を代入して最後の$\sum$の項を消し去れば証明完了です。
(数学的に厳密に行うには和の順序交換や収束生の議論をもっと緻密に行う必要がありますが、ここでは省略)

前の記事の確率分布の歪度に続いて、もう一つ確率分布の形状を表す指標を紹介します。
それは尖度（せんど、kurtosis)という指標です。

これは確率分布関数の鋭さを表す指標で、尖度が大きければ鋭いピークと長く太い裾を持った分布を持ち、
尖度が小さければより丸みがかったピークと短く細い尾を持った分布であるという事が判断できます。
出典:Wikipedia – 尖度

これは次の式で定義されます。($X$:確率変数、$\mu$:期待値、$\sigma$:標準偏差)
最後に3を引いているのは、正規分布の尖度が0となるように定義するためです。

$$
\beta_4 = \frac{E[(X-\mu)^4]}{\sigma^4} – 3
$$

尖度が正ならば、その分布は正規分布よりも尖った分布になります。
(通常の山が一つある形の分布であれば。)

計算は歪度の時と同様に、分子の$E[(X-\mu)^4]$の計算がポイントになりますが、
期待値の線形性により次のように計算できます。

$$
\begin{eqnarray}
E[(X-\mu)^4] &=& E[X^4 – 4X^3\mu + 6X^2\mu^2 – 4X\mu^3 + \mu^4]\\
&=& E[X^4] – 4\mu E[X^3] + 6\mu^2 E[X^2] – 3\mu^4.
\end{eqnarray}
$$

確率分布の特徴を表す値として頻繁に使われるのは期待値と分散(もしくは標準偏差)ですが、
これらの値だけではまだ分布の特徴を完全に捕らえられているとは言えません。
特に、分布を期待値0、分散1に正規化してしまうと、この二つの値だけでは区別がつきませんが、
実際には分布の形が左右非対称に歪んでいたり、中央の尖り具合が違ったりします。

ということで、期待値と分散以外にも、確率分布の形を表す指標があり、その一つが
左右非対称生を示す歪度（わいど,skewness）です。

確率変数$X$に対して、期待値を$\mu$、標準偏差を$\sigma$とすると、次の式で定義されます。

$$
\alpha_3 = \frac{E\left[(X-\mu)^3 \right]}{\sigma^3}
$$

(統計学入門100ページの記号に揃えて、$\alpha_3$と書きましたが、これはどのくらいメジャーなんだろう？
英語版Wikipediaでは、$\gamma_1$が使われてますね。)

山が一つの確率分布であれば、
$\alpha_3>0$の時は右(正の方)の裾が長く、$\alpha_3<0$の時は左(負の方)の裾が長くなります。 具体的な例としては、カイ二乗分布やポアソン分布の歪度は正になります。 実際に計算する時は、分子の$E[(X-\mu)^3]$の計算がポイントになりますが、 これは期待値の線型性を用いて次のように計算します。 $$ \begin{eqnarray} E[(X-\mu)^3] &=& E[X^3 - 3X^2\mu + 3X\mu^2 - \mu^3]\\ &=& E[X^3] - 3\mu E[X^2] + 2\mu^2\\ &=& E[X^3] - 3\mu \sigma^2 - \mu^2. \end{eqnarray} $$ 個人的には3行目の$\sigma$が登場する形より、2行目のモーメントで計算できている形の方が使い勝手が良いと思います。