新年のご挨拶でちょっと書きましたが、このブログが昨年末に攻撃を受けていたようで、過剰なアクセスによりCPUリソースが枯渇する事態となっていました。
下にコンソールで確認したCPUリソースの画像を貼りますが、パーストキャパシティがなくなってますね。この時間帯、ブログの表示が非常に遅くなってしまっていました。最終的にどうやって対策し事象を解消したたかは次の記事に書くとして、この時の状況調査のためにログファイルを確認したのでその時調べたあれこれを記事にまとめておきます。
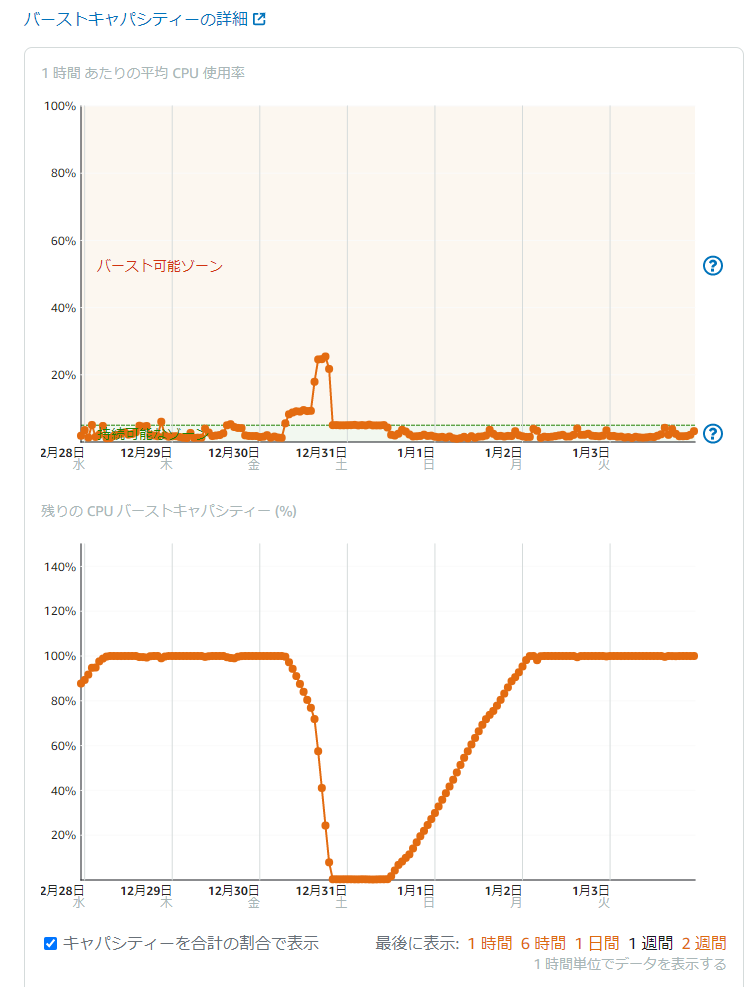
このCPUが異常に利用されていた時なのですが、ブラウザではなくコマンドかプログラムか何かしら機械的なアクセスがされていたようで、Google Analyticsでは特にアクセスの増加等が見られませんでした。GAはブラウザでアクセスしてJavaScriptが動かないとデータが取れませんからね。
ということで、サーバー側のログを調べる必要性が発生したわけです。
通常の構成であれば、apacheのログはデフォルトでは、/var/log/ の配下にあるそうです。
/var/log/apatche か、 /var/log/httpd/ のどちらかの下に。
ただし、LightsailのWordpressはbitnamiというパッケージが使われており、apache自体が通常と違う場所にあって、ログファイルも普通と違う場所にあります。ちなみにapacheがインストールされている場所は次のようにして確認できます。
$ which httpd
/opt/bitnami/apache2/bin/httpd/opt/bitnami の配下にあることがわかりますね。
そして、ログファイルもこの近辺にあります。/opt/bitnami/apache2/log ってディレクトリがあるのです。一応中見ておきますか。
$ ls /opt/bitnami/apache2
bin bnconfig build cgi-bin conf error htdocs icons include logs modules scripts var
$ ls /opt/bitnami/apache2/logs/
access_log access_log-20210801.gz error_log-20200223.gz error_log-20210808.gz
access_log-20200223.gz access_log-20210808.gz error_log-20200302.gz error_log-20210816.g
access_log-20200302.gz access_log-20210816.gz error_log-20200308.gz error_log-20210822.gz
access_log-20200308.gz access_log-20210822.gz error_log-20200316.gz error_log-20210829.gz
#########
# 中略 #
#########
access_log-20210704.gz access_log-20221218.gz error_log-20210712.gz error_log-20221226.gz
access_log-20210712.gz access_log-20221226.gz error_log-20210718.gz error_log-20230101.gz
access_log-20210718.gz access_log-20230101.gz error_log-20210726.gz httpd.pid
access_log-20210726.gz error_log error_log-20210801.gz pagespeed_log名前から明らかですが、access_logがアクセスログで、error_logがエラーログであり、日付がついて拡張子が.gzになっているのがログローテションで圧縮された古いログです。
ちなみにこのログファイルのパスは、次の設定ファイルで設定されています。
$ vim /opt/bitnami/apache2/conf/httpd.conf
# 中略
<IfModule log_config_module>
#
# The following directives define some format nicknames for use with
# a CustomLog directive (see below).
#
LogFormat "%h %l %u %t \"%r\" %>s %b \"%{Referer}i\" \"%{User-Agent}i\"" combined
LogFormat "%h %l %u %t \"%r\" %>s %b" common
<IfModule logio_module>
# You need to enable mod_logio.c to use %I and %O
LogFormat "%h %l %u %t \"%r\" %>s %b \"%{Referer}i\" \"%{User-Agent}i\" %I %O" combinedio
</IfModule>
#
# The location and format of the access logfile (Common Logfile Format).
# If you do not define any access logfiles within a <VirtualHost>
# container, they will be logged here. Contrariwise, if you *do*
# define per-<VirtualHost> access logfiles, transactions will be
# logged therein and *not* in this file.
#
CustomLog "logs/access_log" common
#
# If you prefer a logfile with access, agent, and referer information
# (Combined Logfile Format) you can use the following directive.
#
#CustomLog "logs/access_log" combined
</IfModule>
# 中略
#
# ErrorLog: The location of the error log file.
# If you do not specify an ErrorLog directive within a <VirtualHost>
# container, error messages relating to that virtual host will be
# logged here. If you *do* define an error logfile for a <VirtualHost>
# container, that host's errors will be logged there and not here.
#
ErrorLog "logs/error_log"
#
# LogLevel: Control the number of messages logged to the error_log.
# Possible values include: debug, info, notice, warn, error, crit,
# alert, emerg.
#
LogLevel warnCustomLog / ErrorLog がファイルパスの指定で、LogFormatとしてログの出力書式も指定されていますね。
書式の%hとかの意味はこちらのドキュメントにあります。
参考: mod_log_config – Apache HTTP サーバ バージョン 2.4
あとは中身を確認したら良いです。access_log とかのファイルはapacheがアクセスがあるたびにバリバリ書き込んでる物なので、ロックがかからないようにこれを直接開くのは避けて、どこかにコピーして開きましょう。scp等でローカルに持ってきちゃうのが良いと思います。
拡張子が.gzのものは、gzip コマンドに -d オプションをつけて実行すると解答できます。
# *(アスタリスク)を使ってまとめて解凍しちゃうと楽。
$ gzip -d *.gz
# .gzファイルが無くなり、解凍済みファイルだけが残ります。あとはただのテキストファイルなので、出来上がったファイルを確認したら良いです。
この結果、冒頭に挙げた攻撃を受けてた時間帯は、ログインを試みるアクセスが特定のIPアドレスから7万回も発生していたのがわかりました。
基本的に通常のアクセス分析はGoogle Analyticsを見れば済む話なのでapacheのログに意識をはらってきませんでしたが、今回調査してみてもっと使いやすいフォーマットで出力するように設定しておけば良かったなと思いました。csvではないのでpandasでのパースも面倒でしたし、User Agentなど取れるはずなのに取ってない情報も多かったので。そしてタイムゾーンも日本時間じゃないんですよね。これも地味に扱いにくいです。